3. Sequences of Numbers
3.1. Sequences
So far we have introduced sets as well as the number systems that we will use in this text. Next, we will study sequences of numbers. Sequences are, basically, countably many numbers arranged in an order that may or may not exhibit certain patterns. Here is the formal definition of a sequence:| Definition 3.3.1: Sequence | |
A sequence of real numbers is a function
f: N 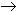 R.
In other words, a sequence can be written as
f(1), f(2), f(3), ..... Usually, we will denote such a sequence
by the symbol R.
In other words, a sequence can be written as
f(1), f(2), f(3), ..... Usually, we will denote such a sequence
by the symbol 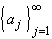 , where
aj = f(j). , where
aj = f(j).
| |
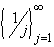 .
Keep in mind that despite the
strange notation, a sequence can be thought of as an ordinary function.
In many cases that may not be the most expedient way to look at the situation. It
is often easier to simply look at a sequence as a 'list' of numbers that may or
may not exhibit a certain pattern.
.
Keep in mind that despite the
strange notation, a sequence can be thought of as an ordinary function.
In many cases that may not be the most expedient way to look at the situation. It
is often easier to simply look at a sequence as a 'list' of numbers that may or
may not exhibit a certain pattern.
We now want to describe what the long-term behavior, or pattern, of a sequence is, if any.
| Definition 3.1.2: Convergence | |
A sequence 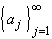 of real (or
complex) numbers is said to converge to a real (or complex) number
c if for every of real (or
complex) numbers is said to converge to a real (or complex) number
c if for every  > 0
there is an integer N > 0 such that if j > N then > 0
there is an integer N > 0 such that if j > N then
| aj - c | <The number c is called the limit of the sequence 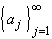 and we sometimes write
aj and we sometimes write
aj 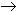 c. c.
If a sequence | |
We are going to establish several properties of convergent sequences, most of
which are probably familiar to you. Many proofs will use an
' argument' as in the proof of the next result.
This type of argument is not easy to get used to, but it will appear again and
again, so that you should try to get as familiar with it as you can.
argument' as in the proof of the next result.
This type of argument is not easy to get used to, but it will appear again and
again, so that you should try to get as familiar with it as you can.
Proposition 3.1.4: Convergent Sequences are Bounded
| |
Let | 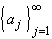 be a convergent
sequence. Then the sequence is bounded, and the limit is unique. be a convergent
sequence. Then the sequence is bounded, and the limit is unique.
| |
| Proposition 3.1.6: Algebra on Convergent Sequences | |
Suppose 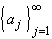 and and
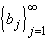 are converging to
a and b, respectively.
Then are converging to
a and b, respectively.
Then
| |
This theorem states exactly what you would expect to be true. The proof of it employs the standard trick of 'adding zero' and using the triangle inequality. Try to prove it on your own before looking it up.
Note that the fourth statement is no longer true for strict inequalities. In other words, there are convergent sequences with an < bn for all n, but strict inequality is no longer true for their limits. Can you find an example ?
While we now know how to deal with convergent sequences, we still need an easy criteria that will tell us whether a sequence converges. The next proposition gives reasonable easy conditions, but will not tell us the actual limit of the convergent sequence.
First, recall the following definitions:
| Definition 3.1.7: Monotonicity | |
A sequence 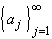 is called monotone increasing if
aj + 1
is called monotone increasing if
aj + 1 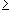 aj for all
j. aj for all
j.
A sequence | |
- Monotone increasing:
-
aj + 1
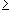 aj
aj
-
aj + 1 - aj
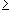 0
0
-
aj + 1 / aj
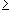 1, if aj > 0
1, if aj > 0
-
aj + 1
- Monotone decreasing:
-
aj + 1
 aj
aj
-
aj + 1 - aj
 0
0
-
aj + 1 / aj
 1, if aj > 0
1, if aj > 0
-
aj + 1
- If a sequence
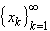 is
bounded above, then c = sup(xk) is finite. Moreover,
given any
is
bounded above, then c = sup(xk) is finite. Moreover,
given any  > 0, there exists
at least one integer k such that
xk > c -
> 0, there exists
at least one integer k such that
xk > c -  , as
illustrated in the picture.
, as
illustrated in the picture.
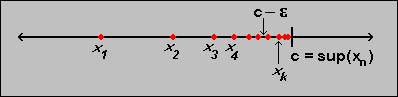
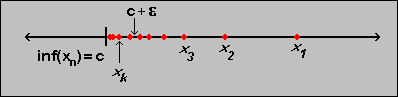
- If a sequence
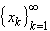 is
bounded below, then c = inf(xk) is finite. Moreover,
given any
is
bounded below, then c = inf(xk) is finite. Moreover,
given any  > 0, there
exists at least one integer k such that
xk < c +
> 0, there
exists at least one integer k such that
xk < c +  ,
as illustrated in the picture.
,
as illustrated in the picture.
| Proposition 3.1.9: Monotone Sequences | |
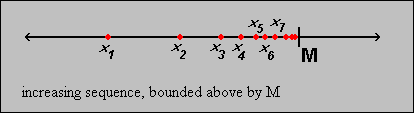
If  is a monotone
increasing sequence that is bounded above, then the sequence must converge. is a monotone
increasing sequence that is bounded above, then the sequence must converge.
If 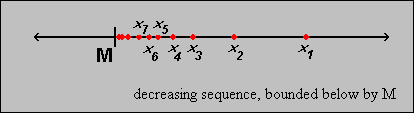
| |
Using this result it is often easy to prove convergence of a sequence just by showing that it is bounded and monotone. The downside is that this method will not reveal the actual limit, just prove that there is one.
| Examples 3.1.10: | |
| |
| Theorem 3.1.11: The Pinching Theorem | |
Suppose {aj} and {cj} are
two convergent sequences such that
lim aj = lim cj = L. If a sequence
{bj} has the property that
ajfor all j, then the sequence {bj} converges and lim bj = L. | |
| Example 3.1.12: | |
|
| |
 Interactive Real Analysis
Interactive Real Analysisj}.gif) does not converge. Prove it.
does not converge. Prove it.
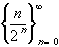 converges to zero Prove it.
converges to zero Prove it.
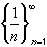 monotone increasing or decreasing ?
monotone increasing or decreasing ?
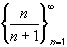 monotone increasing or decreasing ?
monotone increasing or decreasing ?