3. Sequences of Numbers
3.2. Cauchy Sequences
What is slightly annoying for the mathematician (in theory and in praxis) is that we refer to the limit of a sequence in the definition of a convergent sequence when that limit may not be known at all. In fact, more often then not it is quite hard to determine the actual limit of a sequence.We would prefer to have a definition which only includes the known elements of the particular sequence in question and does not rely on the unknown limit. Therefore, we will introduce the following definition:
| Definition 3.2.1: Cauchy Sequence | |
Let 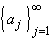 be a sequence of real (or
complex) numbers. We say that the sequence satisfies the Cauchy criterion (or
simply is Cauchy) if for each be a sequence of real (or
complex) numbers. We say that the sequence satisfies the Cauchy criterion (or
simply is Cauchy) if for each
 > 0 there is an integer
N > 0 such that if j, k > N then > 0 there is an integer
N > 0 such that if j, k > N then
| aj - ak | < | |
| Theorem 3.2.2: Completeness Theorem in R | |
Let 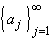 be a Cauchy sequence of
real numbers. Then the sequence is bounded. be a Cauchy sequence of
real numbers. Then the sequence is bounded.
Let | |
Thus, by considering Cauchy sequences instead of convergent sequences we do not need to refer to the unknown limit of a sequence, and in effect both concepts are the same.
Note that the Completeness Theorem not true if we consider only rational numbers. For example, the sequence 1, 1.4, 1.41, 1.414, ... (convergent to the square root of 2) is Cauchy, but does not converge to a rational number. Therefore, the rational numbers are not complete, in the sense that not every Cauchy sequence of rational numbers converges to a rational number.
Hence, the proof will have to use that property which distinguishes the reals from the rationals: the least upper bound property.
 Interactive Real Analysis
Interactive Real Analysis