3.1. Sequences
Proposition 3.1.9: Monotone Sequences
If 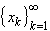 is a monotone
increasing sequence that is bounded above, then the sequence must
converge (see picture).
is a monotone
increasing sequence that is bounded above, then the sequence must
converge (see picture).
If 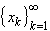 is a monotone
decreasing sequence that is bounded below, then the sequence must converge
(see picture).
is a monotone
decreasing sequence that is bounded below, then the sequence must converge
(see picture).
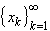 is a monotone
increasing sequence that is bounded above, then the sequence must
converge (see picture).
is a monotone
increasing sequence that is bounded above, then the sequence must
converge (see picture).

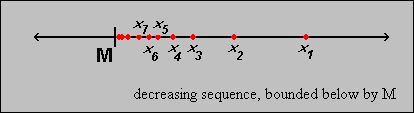
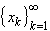 is a monotone
decreasing sequence that is bounded below, then the sequence must converge
(see picture).
is a monotone
decreasing sequence that is bounded below, then the sequence must converge
(see picture).

Proof:
Let's look at the first statement, i.e. the sequence in monotone increasing. Take an > 0 and let
c = sup(xk). Then c is finite, and given
> 0 and let
c = sup(xk). Then c is finite, and given
 > 0, there exists at least
one integer N such that
xN > c -
> 0, there exists at least
one integer N such that
xN > c -  .
Since the sequence is monotone increasing, we then have that
.
Since the sequence is monotone increasing, we then have that
xk > c -for all k > N, or
| c - xk | <for all k > N. But that means, by definition, that the sequence converges to c.
The proof for the infimum is very similar, and is left as an exercise.
 Interactive Real Analysis
Interactive Real Analysis