7. The Integral
7.1. Riemann Integral
In a calculus class integration is introduced as 'finding the
area under a curve'. While this interpretation is certainly useful,
we instead want to think of 'integration' as more sophisticated form of
summation. Geometric considerations, in our situation, will not
be so fruitful, whereas the summation interpretation of integration
will make many of its properties easy to remember.
First, as usual, we need to define integration before we can discuss
its properties. We will start with defining the Riemann integral and we will
move to the more technical but also more flexible Lebesgue integral
later.
| Definition 7.1.1: Partition of an Interval |
| |
A partition P of the closed interval [a, b]
is a finite set of points
P = { x0, x1, x2, ..., xn}
such that
a = x0 < x1 < x2 <
... < xn-1 < xn = b
The maximum difference between any two consecutive points
of the partition is called the norm or mesh of the partition
and denoted as | P |, i.e.
| P | = max { xj - xj-1, j = 1 ... n }
A refinement of the partition P is another partition
P' that contains all the points from P and some
additional points, again sorted by order of magnitude.
|
| Examples 7.1.2: |
| |
 What is the norm of a partition of 10 equally spaced
subintervals in the interval [0, 2] ?
What is the norm of a partition of 10 equally spaced
subintervals in the interval [0, 2] ?
 What is the norm of a partition of n equally spaced
subintervals in the interval [a, b] ?
What is the norm of a partition of n equally spaced
subintervals in the interval [a, b] ?
 Show that if P' is a refinement of P then
| P' |
Show that if P' is a refinement of P then
| P' |  | P |. | P |.
|
Using these partitions, we can define the following finite sum:
| Definition 7.1.3: Riemann Sums |
| |
If
P = { x0, x1, x2, ..., xn}
is a partition of the closed interval [a, b] and
f is a function defined on that interval, then the
n-th Riemann Sum of f with respect to
the partition P is defined as:
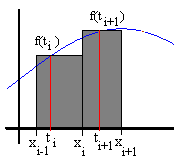
R(f, P) = 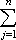 f(tj) (xj - xj-1)
f(tj) (xj - xj-1)
where tj is an arbitrary number in the interval
[xj-1, xj].
|
|
Note: If the function f is positive, a Riemann Sum
geometrically corresponds to a summation of areas of rectangles with
length xj - xj-1 and height
f(tj).
|
| Examples 7.1.4: |
| |
 Suppose f(x) = x2 on [0, 2]. Find
Suppose f(x) = x2 on [0, 2]. Find
- the fifth Riemann sum for an equally spaced partition, taking always the
left endpoint of each subinterval
- the fifth Riemann sum for an equally spaced partition, taking always the
right endpoint of each subinterval
- the n-th Riemann sum for an equally spaced partition,
taking always the right endpoint of each subinterval.
|
Riemann sums have the practical disadvantage that we do not know which point to take
inside each subinterval. To remedy that one could agree to always take the left
endpoint (resulting in what is called the
left Riemann sum) or always
the right one (resulting in the
right Riemann sum). However, it will turn
out to be more useful to single out two other close cousins of Riemann sums:
| Definition 7.1.5: Upper and Lower Sum |
| |
Let
P = { x0, x1, x2, ..., xn}
be a partition of the closed interval [a, b] and
f a bounded function defined on that interval. Then:
- the upper sum of f with respect to the
partition P is defined as:
U(f, P) = 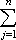 cj (xj - xj-1)
cj (xj - xj-1)
where cj is the supremum of f(x) in
the interval [xj-1, xj].
- the lower sum of f with respect to the
partition P is defined as
L(f, P) = 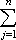 dj (xj - xj-1)
dj (xj - xj-1)
where dj is the infimum of f(x) in the
interval [xj-1, xj].
|
|
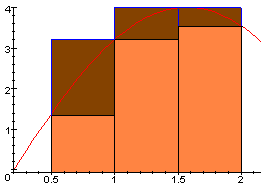
Here is an example where the upper sum in displayed in dark brown
and the lower sum in light brown.
The partition P = {0.5, 1, 1.5, 2}, and the numbers
for the sums are chosen:
- for the upper sum:
c1 = f(1),
c2 = f(1.5), and
c3 = f(1.5)
- for the lower sum:
d1 = f(0.5),
d2 = f(1), and
d3 = f(2)
|
|
| Examples 7.1.6: |
| |
 Suppose f(x) = x2-1 for x in the interval
[-1, 1]. Find:
Suppose f(x) = x2-1 for x in the interval
[-1, 1]. Find:
- The left and right sums where the interval [-1, 1] is
subdivided into 10 equally spaced subintervals.
- The upper and lower sums where the interval [-1, 1]
is subdivided into 10 equally spaced subintervals.
- The upper and lower sums where the interval [-1,1] is subdivided
into n equally spaced subintervals.
 Why is, in general, an upper (or lower) sum not a special case of a Riemann sum ?
Find a condition for a function f so that the upper and lower sums
are actually special cases of Riemann sums.
Why is, in general, an upper (or lower) sum not a special case of a Riemann sum ?
Find a condition for a function f so that the upper and lower sums
are actually special cases of Riemann sums.
 Find conditions for a function so that the upper sum can be computed by always
taking the left endpoint of each subinterval of the partition, or conditions for
always being able to take the right endpoints.
Find conditions for a function so that the upper sum can be computed by always
taking the left endpoint of each subinterval of the partition, or conditions for
always being able to take the right endpoints.
 Suppose f is the Dirichlet function, i.e. the function that is
equal to 1 for every rational number and 0 for every
irrational number. Find the upper and lower sums over the interval [0, 1]
for an arbitrary partition.
Suppose f is the Dirichlet function, i.e. the function that is
equal to 1 for every rational number and 0 for every
irrational number. Find the upper and lower sums over the interval [0, 1]
for an arbitrary partition.
|
These various sums are related via a basic inequality, and they
are also related to a refinement of the partition in the following
theorem:
| Proposition 7.1.7: Size of Riemann Sums |
| |
Suppose
P = { x0, x1, x2, ..., xn}
is a partition of the closed interval [a, b], f a bounded
function defined on that interval. Then we have:
- The lower sum is increasing with respect to refinements of
partitions, i.e.
L(f, P')
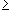 L(f, P) for every refinement
P' of the partition P L(f, P) for every refinement
P' of the partition P
- The upper sum is decreasing with respect to refinements of
partitions, i.e.
U(f, P')
 U(f,P) for every refinement
P' of the partition P U(f,P) for every refinement
P' of the partition P
- L(f, P)
 R(f, P)
R(f, P)  U(f, P) for every partition P
U(f, P) for every partition P
Proof
|
In other words, the lower sum is always less than or equal to the upper sum, and
the upper sum is decreasing with respect to a refinement of the partition while
the lower sum is increasing with respect to a refinement of the partition. Hence,
a natural question is: will the two quantities ever coincide ?
| Definition 7.1.8: The Riemann Integral |
| |
Suppose f is a bounded function defined on a closed, bounded interval
[a, b]. Define the upper and lower Riemann
integrals, respectively, as
I*(f) = inf{ U(f,P): P a partition of [a, b]}
I*(f) = sup{ L(f,P): P a partition of [a, b]}
Then if I*(f) = I*(f) the function
f is called Riemann integrable and the Riemann integral
of f over the interval [a, b] is denoted by
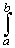 f(x) dx f(x) dx
|
Note that upper and lower sums depend on the particular partition chosen, while
the upper and lower integrals are independent of partitions. However, this
definition is very difficult for practical applications, since we need to find
the
sup and
inf over
any partition.
| Examples 7.1.9: |
| |
 Show that the constant function
f(x) = c is Riemann integrable on any interval [a, b]
and find the value of the integral.
Show that the constant function
f(x) = c is Riemann integrable on any interval [a, b]
and find the value of the integral.
 Is the function f(x) = x2 Riemann integrable on the
interval [0,1] ? If so, find the value of the Riemann
integral. Do the same for the interval [-1, 1].
Is the function f(x) = x2 Riemann integrable on the
interval [0,1] ? If so, find the value of the Riemann
integral. Do the same for the interval [-1, 1].
 Is the Dirichlet function Riemann integrable on the interval [0, 1] ?
Is the Dirichlet function Riemann integrable on the interval [0, 1] ?
|
The third example shows that not every function is Riemann integrable, and
the second one shows that we need an easier condition to determine
integrability of a given function. The next lemma provides such a condition for
integrability.
| Examples 7.1.11: |
| |
 Is the function f(x) = x2 Riemann integrable on the interval
[0,1] ? If so, find the value of the Riemann integral. Do the same for
the interval [-1, 1] (since this is the same example as before, using
Riemann's Lemma will hopefully simplify the solution).
Is the function f(x) = x2 Riemann integrable on the interval
[0,1] ? If so, find the value of the Riemann integral. Do the same for
the interval [-1, 1] (since this is the same example as before, using
Riemann's Lemma will hopefully simplify the solution).
 Suppose f is Riemann integrable over an interval
[-a, a] and { Pn } is a sequence
of partitions whose mesh converges to zero. Show that for any Riemann sum
we have
Suppose f is Riemann integrable over an interval
[-a, a] and { Pn } is a sequence
of partitions whose mesh converges to zero. Show that for any Riemann sum
we have
lim R(f, Pn) = 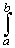 f(x) dx f(x) dx
 Suppose f is Riemann integrable over an interval
[-a, a] and f is an odd function, i.e.
f(-x) = -f(x). Show that the integral of f over
[-a, a] is zero. What can you say if f is an even
function?
Suppose f is Riemann integrable over an interval
[-a, a] and f is an odd function, i.e.
f(-x) = -f(x). Show that the integral of f over
[-a, a] is zero. What can you say if f is an even
function?
|
Now we can state some easy conditions that the Riemann integral satisfies. All
of them are easy to memorize if one thinks of the Riemann integral as a somewhat
glorified summation.
| Examples 7.1.13: |
| |
 Find an upper and lower estimate for
Find an upper and lower estimate for
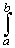 x sin(x) dx over the
interval [0, 4]. x sin(x) dx over the
interval [0, 4].
 Suppose f(x) = x2 if x
Suppose f(x) = x2 if x  1
and f(x) = 3 if x > 1. Find 1
and f(x) = 3 if x > 1. Find
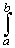 f(x) dx over the interval
[-1, 2]. f(x) dx over the interval
[-1, 2].
 If f is an integrable function defined on [a, b] which is bounded by
M on that interval, prove that
If f is an integrable function defined on [a, b] which is bounded by
M on that interval, prove that
M (a - b) 
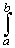 f(x) dx f(x) dx
 M (b - a)
M (b - a)
|
Now we can illustrate the relation between Riemann integrable and
continuous functions.
Note that this theorem does not say anything about the actual value of the
Riemann integral. Also, we have as a free extra condition that that f
is bounded, since every continuous function on a compact set is automatically
bounded.
Since differentiable functions are continuous, this result implies that
{ differentiable functions }
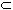 { continuous functions }
{ continuous functions }
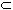 { integrable functions }
{ integrable functions }
and each set is in fact a proper subset of the next.
| Examples 7.1.15: |
| |
 Find a function that is not integrable, a function that is integrable but not
continuous, and a function that is continuous but not differentiable.
Find a function that is not integrable, a function that is integrable but not
continuous, and a function that is continuous but not differentiable.
|
To finalize the relation between integrable and continuous functions, the
following theorem can be proved (but it uses the concept of a
measure, defined later):
| Theorem 7.1.16: Lebesgue's Theorem |
| |
If f is a bounded function defined on a closed, bounded interval
[a, b] then f is Riemann integrable if and only if
the set of points where f is discontinuous has measure zero.
Proof
|
A set of measure zero, as we will see later, is any set of finitely or countably many points.
Therefore, we could rephrase the above exact theorem as follows:
The converse is not quite true: If f is a bounded function defined on
a closed, bounded interval [a, b] and f is Riemann
integrable, then f is continuous on [a, b]
except possibly at a set of measure zero, but a set of measure zero does not necessarily
consist of countably many points.
| Examples 7.1.18: |
| |
 Show that every monotone function defined on [a, b] is Riemann integrable.
Show that every monotone function defined on [a, b] is Riemann integrable.
 Let g(x) = 0 if x is irrational and g(p/q) = 1/q if
x = p/q is rational, p, q relatively prime and q > 0,
and assume g is restricted to [0, 1]. Is g Riemann
integrable ? If so, what is the value of the integral ?
Let g(x) = 0 if x is irrational and g(p/q) = 1/q if
x = p/q is rational, p, q relatively prime and q > 0,
and assume g is restricted to [0, 1]. Is g Riemann
integrable ? If so, what is the value of the integral ?
|
Now that we have easy conditions to determine which functions are integrable,
it would also be convenient to have a nice shortcut to easily compute the
actual value of an integral.
| Theorem 7.1.19: Fundamental Theorem of Calculus |
| |
Suppose f is a bounded, integrable function defined on the closed, bounded interval
[a, b], define a new function:
F(x) = 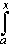 f(t) dt f(t) dt
Then F is continuous in [a, b]. Moreover, if f is also continuous,
then F is differentiable in (a, b) and
F'(x) = f(x) for all x in (a, b)
In many calculus texts this theorem is called the Second
Fundamental Theorem of Calculus.
Proof
|
This theorem has an easy corollary that enables us to quickly find
the value of an integral in many situations.
| Corollary 7.1.20: Integral Evaluation Shortcut |
| |
Suppose f is an continuous function defined on the closed, bounded interval
[a, b], and G is a function on [a, b] such that
G'(x) = f(x) for all x in (a, b). Then
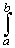 f(x) dx = G(b) - G(a) f(x) dx = G(b) - G(a)
The function G is often called
Antiderivative of f, and this corollary is
called First Fundamental Theorem of Calculus
Proof
|
Before we look at several examples, we should rephrase these results in less
rigorous notation. The first theorem says, basically:
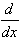
 f(x) dx = f(x)
f(x) dx = f(x)
while the corollary states, basically, that:

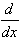 f(x) dx = f(b) - f(a)
f(x) dx = f(b) - f(a)
Hence, loosely speaking, integration and differentiation are inverse
operations of each other.
| Examples 7.1.21: |
| |
 Define a function
F(x) =
Define a function
F(x) = 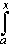 t2 sin(t) dt
for x in the interval [a, a + 10]. t2 sin(t) dt
for x in the interval [a, a + 10].
- Find F(a)
- Find F'(x)
- Find F''(x)
- Find all critical points of F(x) in [a, a + 10]
 Find the value of the following integrals:
Find the value of the following integrals:
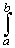 x5 - 4 x2 dx
on the interval [0, 2]. x5 - 4 x2 dx
on the interval [0, 2].
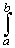 1/x2 + cos(x) dx
on the interval [1, 4]. 1/x2 + cos(x) dx
on the interval [1, 4].
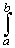 (1 + x2)-1 dx
on the interval [-1, 1]. (1 + x2)-1 dx
on the interval [-1, 1].
 Show that if one starts with an integrable function f in the
Fundamental Theorem of Calculus that is not continuous, the corresponding
function F may not be differentiable.
Show that if one starts with an integrable function f in the
Fundamental Theorem of Calculus that is not continuous, the corresponding
function F may not be differentiable.
|
In the next chapter we will learn some more shortcuts to compute the value of an
integral called
substitution method and
integration by parts.


 > 0 there exists at least one partition
P such that
> 0 there exists at least one partition
P such that
{ continuous functions }
{ integrable functions }
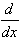
f(x) dx = f(x)

f(x) dx = f(b) - f(a)
 Interactive Real Analysis
Interactive Real Analysis | P |.
| P |.
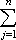 f(tj) (xj - xj-1)
f(tj) (xj - xj-1)
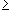 L(f, P) for every refinement
P' of the partition P
L(f, P) for every refinement
P' of the partition P
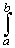 f(x) dx
f(x) dx
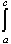 f(x) dx +
f(x) dx +
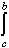 f(x) dx
f(x) dx
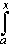 f(t) dt
f(t) dt