3.1. Sequences

Examples 3.1.10(c): Computing Square Roots

Let a > 0 and x0 > 0 and define the recursive sequence
xn+1 = 1/2 (xn + a / xn)
Show that this sequence converges to the square root of a regardless of the starting point x0 > 0.
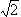Before giving the proof, let's see how this recursive sequence can be used to compute a square root very efficiently. Let's say we want to compute . Let's start with x0 = 2. Note that the 'true' value of 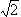with 12 digits after the period is 1.414213562373. Our recursive sequence would approximate this value quickly as follows:

Term Exact Value Approximate Value
x0 2
x1 = 1/2 (x0 + a / x0) 1/2 (2 + 2/2) = 3/2 1.5
x2 = 1/2 (x1 + a / x1) 1/2 (3/2 + 2/3/2) = 17/12 1.416666667
x3 = 1/2 (x2 + a / x2) 1/2 (17/12 + 2/17/12) = 577/408 1.414215686
x4 = 1/2 (x3 + a / x3) 1/2 (577/408 + 2/577/408) = 665857/470832 1.414213562375

After only 4 steps our sequence has approximated the 'true' value of 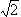with 11 digits accuracy.

Now that we have seen the usefulness of this particular recursive sequence we need to prove that it really does converge to the square root of a.

First, note that xn > 0 for all n so that the sequence is bounded below.

Next, let's see if the sequence is monotone decreasing, in which case it would have to converge to some limit. Compute

xn - xn+1 = xn - 1/2 (xn + a / xn) = 1/2 (xn2 - a) / xn
Now let's take a look at xn2 - a:
xn2 - a = 1/4 (xn-1 + a / xn-1)2 - a
      = 1/4 xn-12 + 1/2 a + 1/4 a2 / xn-12 - a
      = 1/4 xn-12 - 1/2 a + 1/4 a2 / xn-12
      = 1/4 (xn-1 - a / xn-1)2
      0
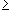But that means that xn - xn+1 0, or equivalently xn 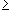xn+1. Hence, the sequence is monotone decreasing and bounded below by 0 so it must converge.

We now know that 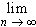xn = L. To find that limit, we could try the following:

(*) L = xn = xn+1 = 1/2 (xn + a/xn) = 1/2 (L + a / L)
Solving the equation L = 1/2 (L + a / L) gives
2 L2 = L2 + a
or equivalently
L2 = a
which means that the limit L is indeed the square root of a, as required.

However, our proof contains one small caveat. In order to take the limit inside the fraction in equation (*) we need to know that L is not zero before we can write down equation (*). We already know that xn is bounded below by zero, but that is not good enough to exclude the possibility of L = 0. But we have already shown that

xn2 - a = 1/4 (xn-1 - a / xn-1)2 0
so that xn2 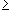a. That implies that the limit of the sequence (which we already know exists) is strictly positive since a > 0. Therefore equation (*) is justified and we have completed the proof.

Next | Previous | Glossary | Map