Interactive Real Analysis3.1. Sequences
Example 3.1.3(a):
The sequence 
converges to zero.
Back
converges to zero.
Back
=
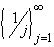{1, 1/2, 1/3, 1/4, ... },
which seems to indicate that the terms are getting closer and
closer to zero. According to the definition of convergence, we
need to show that no matter which
> 0 one chooses,
the sequence will eventually become smaller than this number.
To be precise: take any
> 0. Then there
exists a positive integer N such that
1 / N < .
Therefore, for any j > N we have:
| 1/j - 0 | = | 1/j | < 1/N <whenever j > N. But this is precisely the definition of the sequence {1/j} converging to zero.
While it looks like this proof is easy, it is a good indication
for
'-arguments' that will
appear again and again. In most of those cases the proper choice
of N will make it appear as if the proof works like
magic.