3.2. Cauchy Sequences
Theorem 3.2.2: Completeness Theorem in R
Let 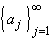 be a
Cauchy sequence of real numbers. Then the sequence is bounded.
be a
Cauchy sequence of real numbers. Then the sequence is bounded.
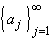 be a
Cauchy sequence of real numbers. Then the sequence is bounded.
be a
Cauchy sequence of real numbers. Then the sequence is bounded.
Let 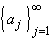 be a
sequence of real numbers. The sequence is Cauchy if and only if it
converges to some limit a.
be a
sequence of real numbers. The sequence is Cauchy if and only if it
converges to some limit a.
Proof:
The proof of the first statement follows closely the proof of the corresponding result for convergent sequences. Can you do it ?To prove the second, more important statement, we have to prove two parts:
First, assume that the sequence converges to some limit a.
Take any  > 0. There
exists an integer N such that if j > N then
| aj - a | <
> 0. There
exists an integer N such that if j > N then
| aj - a | <  /2.
Hence:
/2.
Hence:
| aj - ak |if j, k > N. Thus, the sequence is Cauchy.| aj - a | + | a - ak| < 2
/ 2 =

Second, assume that the sequence is Cauchy (this direction is much harder). Define the set
S = {xSince the sequence is bounded (by part one of the theorem), say by a constant M, we know that every term in the sequence is bigger than -M. Therefore -M is contained in S. Also, every term of the sequence is smaller than M, so that S is bounded by M. Hence, S is a non-empty, bounded subset of the real numbers, and by the least upper bound property it has a well-defined, unique least upper bound. LetR: x < aj for all j except for finitely many}
a = sup(S)We will now show that this a is indeed the limit of the sequence. Take any
 > 0 , and choose
an integer N > 0 such that
> 0 , and choose
an integer N > 0 such that
| aj - ak | <if j, k > N. In particular, we have:/ 2
| aj - aN + 1 | <if j > N, or equivalently/ 2
-Hence we have:/ 2 < aj - aN + 1 <
/ 2
aj > aN + 1 -for j > N. Thus, aN + 1 -/ 2
 / 2
is in the set S, and we have that
/ 2
is in the set S, and we have that
aIt also follows thataN + 1 -
/ 2
aj < aN + 1 +for j > N. Thus, aN + 1 +/ 2
 / 2
is not in the set S, and therefore
/ 2
is not in the set S, and therefore
aBut now, combining the last several line, we have that:aN + 1 +
/ 2
|a - aN + 1 | <and together with the above that results in the following:/ 2
| a - aj | < |a - aN + 1 | + | aN + 1 - aj | < 2for any j > N./ 2 =

Contributed to this page: Lakshmi Natarajan
 Interactive Real Analysis
Interactive Real Analysis