7.1. Riemann Integral
Examples 7.1.18(b):
Let
We have seen this function before, where we have shown that
it is continuous at all irrational numbers and discontinuous
at the rationals. In particular, the function has countably
many points of discontinuity. Since the discontinuities are dense, i.e.
they are "all over" the interval [0, 1] it might seem
that it is difficult to find the value of the integral (if the function
is Riemann integrable). But with the theoretical background we
developed so far it will be easy to compute the answer.
where p, q relatively prime and q > 0, and assume g is restricted to [0, 1]. Is g Riemann integrable ? If so, what is the value of the integral ?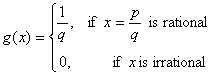
Having countably many discontinuities, we know by our previous theorem that the function is Riemann integrable and it remains to find the value of the integral.
Take any partition P = {x0, x1, ..., xn} and look at:
dj = inf{g(x): xSince every subinterval [xj-1, xj] contains irrational numbers we clearly have that dj = 0 for all j. But then the lower integral I*(g) = sup{ L(g,P): P a partition of [a, b]} must also be 0.[xj-1, xj]}
Since g was integrable the upper and lower integral agree so that
for a = 0 and b = 1.g(x) dx = 0
 Interactive Real Analysis
Interactive Real Analysis