7.1. Riemann Integral
Proposition 7.1.7: Size of Riemann Sums
Suppose
P = { x0, x1, x2, ..., xn}
is a partition of the closed interval [a, b], f a bounded
function defined on that interval. Then we have:
- The lower sum is increasing with respect to refinements of
partitions, i.e.
L(f, P')
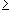 L(f, P)
for every refinement P' of the partition
P
L(f, P)
for every refinement P' of the partition
P
- The upper sum is decreasing with respect to refinements of
partitions, i.e. U(f, P')
 U(f,P)
for every refinement P' of the partition
P
U(f,P)
for every refinement P' of the partition
P
-
L(f, P)
 R(f, P)
R(f, P)  U(f, P) for every partition P
U(f, P) for every partition P
Proof:
The last statement is simple to prove: take any partition P = {x0, x1, ..., xn}. Theninf{ f(x), xj-1where tj is an arbitrary number in [xj-1, xj] and j = 1, 2, ..., n. That immediately implies thatx
xj }
f(tj)
sup{ f(x), xj-1
x
xj }
L(f, P)R(f, P)
U(f, P)
The other statements are somewhat trickier. Let's first find out why they should be true. To make it simple, let's say that P = {a, b} and P' = {a, x0, b}. Then
U(f, P) = sup{ f(x), xand the upper sum for P' would be[a, b] } × (b - a)
U(f, P') = sup{ f(x), xGeometrically, the upper sum for P corresponds to one large rectangle, the one for P' to two smaller rectangles, where the smaller rectangles fit into the larger one but do not cover it.[a, x0] } × (x0 - a) + sup{ f(x), x
[x0, b] } × (b - x0)
|
|
|
Let's show this mathematically, in case one additional point t0 is added to a particular subinterval [xj-1, xj]. Let:
- cj be the sup of f(x) in the interval [xj-1, xj]
- Aj be the sup of f(x) in the interval [xj-1, t0]
- Bj be the sup of f(x) in the interval [t0, xj]
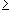 Aj
and
cj
Aj
and
cj 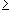 Bj
so that
Bj
so that
cj (xj - xj-1) = cj (xj - t0 + t0 - xj-1) = cj (xj - t0) + cj (t0 - xj-1)That shows that if P = {x0, ... xj-1, xj, ..., xn} and P' = {x0, ... xj-1, t0, xj, ..., xn} then U(f, P)
Bj (xj - t0) + Aj (x0 - tj-1)
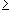 U(f, P').
U(f, P').
The proof for a general refinement P' of P uses the same idea plus some confusing indexing scheme. No more details should be necessary.
The proof for the statement regarding the lower sum is analogous.
 Interactive Real Analysis
Interactive Real Analysis