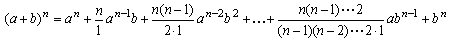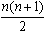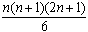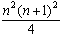2. Infinity and Induction
2.3. The Principle of Induction
In this section we will briefly review a common technique for many mathematical proofs
called the Principle of Induction. Based on this principle there is a constructive method
called Recursive Definition that is also used in several proofs. Both principles, in fact,
can be applied to many well-ordered sets.
| Examples 2.3.2: |
| |
 Determine which of the following sets and their ordering relations are
partially ordered, ordered, or well-ordered:
Determine which of the following sets and their ordering relations are
partially ordered, ordered, or well-ordered:
- S is any set. Define a
 b if
a = b b if
a = b
- S is any set, and P(S) the power set of S.
Define A
 B if
A B if
A 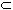 B B
- S is the set of real numbers between [0, 1]. Define
a
 b if a is less than or equal to b
(i.e. the 'usual' interpretation of the symbol b if a is less than or equal to b
(i.e. the 'usual' interpretation of the symbol  ) )
- S is the set of real numbers between [0, 1]. Define
a
 b if a is greater than or equal to b. b if a is greater than or equal to b.
 Which of the following sets are well-ordered ?
Which of the following sets are well-ordered ?
- The number systems N, Z, Q, or R ?
- The set of all rational numbers in [0, 1] ?
- The set of positive rational numbers whose denominator equals 3 ?
|
| Theorem 2.3.3: Induction Principle |
| |
Let S be a well-ordered set with the additional
property that every element except for the smallest one has an
immediate predecessor. Then: if Q is a property such that:
- the smallest element of S has the property Q
- if s
 S has property Q
then the successor of s also has property Q S has property Q
then the successor of s also has property Q
Then the property Q holds for every element in S
Proof
|
Recall the this is very similar to parts of the Peano Axioms,
and it is easy to see that the principle of induction applies
to the well-ordered set of natural numbers.
To use the principle of induction for the natural numbers one has to proceed in four
steps:
- Define a property that you believe to be true for some ordered set (such as
N)
- Check if the property is true for the smallest number of your set
(1 for N)
- Assume that property is true for an arbitrary element of your set
(n for N)
- Prove that the property is still true for the successor of that element
(n+1 for N)
| Examples 2.3.4: |
| |
 Use induction to prove the following statements:
Use induction to prove the following statements:
- The sum of the first n positive integers is n (n+1) / 2.
- If a, b > 0, then
(a + b) n
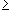 an + bn
for any positive integer n. an + bn
for any positive integer n.
 Use induction to prove Bernoulli's inequality:
Use induction to prove Bernoulli's inequality:
- If x
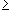 -1 then
(1 + x) n -1 then
(1 + x) n 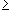 1 + n x for all positive
integers n 1 + n x for all positive
integers n
|
Before stating a theorem whose proof is based on the induction principle,
we should find out why the additional property that every element except
the smallest one must have an immediate predecessor is necessary for the
induction principle:
| Example 2.3.5: |
| |
 The set of natural numbers, with the usual ordering, is well-ordered,
and in addition every element except of 1 has an immediate predecessor.
Now impose a different ordering labeled << on the natural
numbers:
The set of natural numbers, with the usual ordering, is well-ordered,
and in addition every element except of 1 has an immediate predecessor.
Now impose a different ordering labeled << on the natural
numbers:
- if n and m are both even, then define
n << m if n < m
- if n and m are both odd, then define
n << m if n < m
- if n is even and m is odd, we always define
n << m
Is the set of natural numbers, together with this new ordering
<< well-ordered ? Does it have the property that every
element has an immediate predecessor ?
 Suppose the induction principle defined above does not contain the
assumption that every element except for the smallest has an immediate
predecessor. Then show that it could be proved that every natural
number must be even (which is, of course, not true so the additional
assumption on the induction principle is necessary).
Suppose the induction principle defined above does not contain the
assumption that every element except for the smallest has an immediate
predecessor. Then show that it could be proved that every natural
number must be even (which is, of course, not true so the additional
assumption on the induction principle is necessary).
|
A somewhat more complicated, but very useful theorem that can be proved by induction is
the binomial theorem:
Based on the Induction principle is the principle of Recursive Definition that is used
frequently in computer science.
| Definition 2.3.7: Recursive Definition |
| |
Let S be a set. If we define a function h from N to S
as follows:
- h(1) is a uniquely defined element of S
- h(n) is defined via a formula that involves at most terms
h(j) for 0 < j < n
Then this construction determines a unique function h from N
to S.
|
| Examples 2.3.8: |
| |
 Below are two recursive definitions, only one of which is valid. Which one is the
valid one ?
Below are two recursive definitions, only one of which is valid. Which one is the
valid one ?
- Let
x0 = x1 = 1 and define
xn = xn - 1 + xn - 2 for all n > 1.
- Select the following subset from the natural numbers:
- x0 = smallest element of N
- xn = smallest element of
[N - {x0 , x1 , x2 , ..., xn + 1}]
|
When first encountering proofs by induction, it seems that anything can be proved. It is
hard, in fact almost impossible, to find out why a particular property should be true when
looking at an induction proof, and therefore, one might use induction to prove anything
(Incidentally, such proofs are often called non-constructive proofs).
| Exercise 2.3.9: |
| |
 Try to use induction to prove that the sum of the first n square
numbers is equal to (n + 2)/3. (This induction proof should fail, since the
statement is false - or is it true ?)
Try to use induction to prove that the sum of the first n square
numbers is equal to (n + 2)/3. (This induction proof should fail, since the
statement is false - or is it true ?)
|
Here is a more elaborate example of an invalid induction proof:
"Proof"
- The property is clearly true for n = 1, because �one bird is of the same
color'.
- Assume that n birds are of the same color.
- Now take (n+1) birds. Put one aside. There are n birds left, which,
by assumption, are of the same color. For simplicity, say they are all black. Put the
one bird back into the group, and take out another one. Again, there are n birds
remaining, which by assumption must have the same color. In particular, the bird that
was taken out in the first place must now have the same color as all the other birds,
namely black. The bird taken outside was also black. Therefore, the n+1 birds
must all be black.
- But that means that we have proved property Q for all natural numbers by
induction. Yet, the statement is obviously wrong. Where does this proof actually break
down ?
A similar word of caution applies to Recursive Definitions. While that principle can be
very useful, one has to be careful not to get into logical difficulties.
| Example 2.3.11: |
| |
- A classical example for a recursive definition that does not work is the paradox
of the barber of Seville: The barber of Seville is that inhabitant of Seville who shaves
every man in Seville that does not shave himself.
 The problem here is: who shaves the barber ?
The problem here is: who shaves the barber ?
|
To conclude, let's prove two more 'theorems' via induction:
| Examples 2.3.12: Sum of Squares and Cubes |
| |
 Prove the following statements via induction:
Prove the following statements via induction:
- The sum of the first n numbers is equal
to
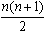
- The sum of the first n square numbers is
equal to
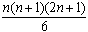
- The sum of the first n cubic numbers is
equal to
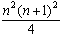
|
Contributed to this page:
Thomas Wollmann
 ) between S and
itself such that the following conditions are satisfied:
) between S and
itself such that the following conditions are satisfied:
 Interactive Real Analysis
Interactive Real Analysis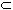 B
B
 S has property Q
then the successor of s also has property Q
S has property Q
then the successor of s also has property Q
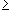 an + bn
for any positive integer n.
an + bn
for any positive integer n.