2.3. The Principle of Induction
Examples 2.3.2(a):
- S is any set. Define
a
 b if a = b
b if a = b
- S is any set, and P(S) the power set of S.
Define A
 B if
A
B if
A 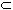 B
B
- S is the set of real numbers between [0, 1]. Define
a
 b if a is less than or equal
to b (i.e. the 'usual' interpretation of the symbol
b if a is less than or equal
to b (i.e. the 'usual' interpretation of the symbol
 )
)
- S is the set of real numbers between [0, 1]. Define
a
 b if a is greater than or
equal to b.
b if a is greater than or
equal to b.
 b if
a = b.
b if
a = b. This is a trivial partial ordering. Since no element is related to an element different from itself, this is not an ordered set. Without more information about S we can not determine anything else.
This example shows that any set can be partially ordered.
2. S is any set, and P(S) the power set of S. Define
A  B if
A
B if
A 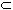 B
B
Recall that if A 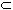 B and
B
B and
B 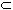 A then A = B.
Therefore, this is indeed a partial ordering. Without more information about
the set S we can not determine anything else.
A then A = B.
Therefore, this is indeed a partial ordering. Without more information about
the set S we can not determine anything else.
3. S is the set of real numbers between [0, 1]. Define
a  b if a is less than or
equal to b (i.e. the 'usual' interpretation of the symbol
b if a is less than or
equal to b (i.e. the 'usual' interpretation of the symbol
 )
)
This is clearly an ordering, and the set [0, 1] with this ordering is usually represented as a subset of the number line. It is not a well-ordered set, because the subset (0,1] has no smallest element.
4. S is the set of real numbers between [0, 1]. Define
a  b if a is greater than or
equal to b.
b if a is greater than or
equal to b.
This is also an ordering. The set is not well-ordered, however, because the
subset [0, 1) has no smallest element. Note that 1 is the smallest element in
the set [0, 1), according to our convention. Here it is important to
distinguish between the conventional meaning of the symbol
 and its meaning as we choose
to define it for a particular situation.
and its meaning as we choose
to define it for a particular situation.
 Interactive Real Analysis
Interactive Real Analysis