Interactive Real Analysis

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 5.1. Open and Closed Sets
• 5.2. Compact and Perfect Sets
• 5.3. Connected and Disconnected Sets
• 6. Limits, Continuity, and Differentiation
• 7. The Integral
• 8. Sequences of Functions
• 9. Historical Tidbits
• Java Tools

5.2. Compact and Perfect Sets

Examples 5.2.5(c):

Let S = (0, 1). Define a collection C = { (1/j, 1), for all j > 0 }. Is C an open cover for S ? How many sets from the collection C are actually needed to cover S ?

Back

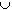• (1 / j, 1) = (0, 1)

Not all sets from the original collection C are needed to cover S. For example, the subcollection of intervals (1 / (2 j) , 1) is also an open covering. However, we can not reduce this cover to a finite subcovering. To see this, extract finitely many sets of the form (1 / j , 1) from the collection C. Let N be the largest integer j that occurs in this subcollection. Then the point 1 / (N + 1) is in S, but it is not in any of the intervals of the finite subcollection. Hence, no finite subcollection from C can cover S.

On the other hand, S does have some other finite open coverings. For example, the collection { (-1, 1/2), (0, 2) } is such a finite open cover. However, the giving open covering C from above can not be reduced to a finite subcover.