5. Topology
5.3. Connected and Disconnected Sets
In the last two section we have classified the open sets, and looked at two classes of
closed set: the compact and the perfect sets. In this section we will introduce two other
classes of sets: connected and disconnected sets.
Note that the definition of disconnected set is easier for an open set
S. In
principle, however, the idea is the same: If a set
S can be separated into two
open, disjoint sets in such a way that neither set is empty and both sets combined give the
original set
S, then
S is called disconnected.
To show that a set is disconnected is generally easier than showing connectedness: if you
can find a point that is not in the set S, then that point can often be used to
'disconnect' your set into two new open sets with the above properties.
| Examples 5.3.2: |
| |
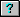 Is the set { x
Is the set { x 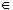 R : | x | < 1, x # 0 }
connected or disconnected ? What about the set
{ x R : | x | < 1, x # 0 }
connected or disconnected ? What about the set
{ x 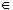 R : | x | R : | x |
 1, x # 0 } 1, x # 0 }
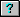 Is the set [-1, 1] connected or disconnected ?
Is the set [-1, 1] connected or disconnected ?
 Is the set of rational numbers connected or disconnected ? How about the irrationals ?
Is the set of rational numbers connected or disconnected ? How about the irrationals ?
 Is the Cantor set connected or disconnected ?
Is the Cantor set connected or disconnected ?
|
In the real line connected set have a particularly nice description:
Hence, as with open and closed sets, one of these two groups of sets are easy:
- open sets in R are the union of disjoint open intervals
- connected sets in R are intervals
The other group is the complicated one:
- closed sets are more difficult than open sets (e.g. Cantor set)
- disconnected sets are more difficult than connected ones (e.g. Cantor set)
In fact, a set can be disconnected at every point.
Intuitively, totally disconnected means that a set can be be broken up into two pieces at
each of its points, and the breakpoint is always 'in between' the original set.
| Example 5.3.5: |
| |
 The Cantor set is disconnected. Is it totally disconnected ?
The Cantor set is disconnected. Is it totally disconnected ?
 Is the set {0, 1} connected or disconnected ? Is it totally disconnected ?
Is the set {0, 1} connected or disconnected ? Is it totally disconnected ?
 Is the set {1, 1/2, 1/3, 1/4, ...} totally disconnected ? How about the set
{1, 1/2, 1/3, 1/4 ...}
Is the set {1, 1/2, 1/3, 1/4, ...} totally disconnected ? How about the set
{1, 1/2, 1/3, 1/4 ...} 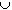 {0} ? {0} ?
 Find a totally disconnected subset of the interval [0, 1] of length 0 (different
from the Cantor set), and another one of length 1.
Find a totally disconnected subset of the interval [0, 1] of length 0 (different
from the Cantor set), and another one of length 1.
|
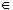 S there exist disjoint open set
U and V such that x
S there exist disjoint open set
U and V such that x 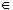 U,
y
U,
y 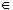 V, and (U
V, and (U
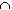 S)
S)
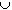 (V
(V  S) = S.
S) = S.
 Interactive Real Analysis
Interactive Real Analysis 1, x # 0 }
1, x # 0 }