5.2. Compact and Perfect Sets
Example 5.2.13(d): Properties of the Cantor Set
The Cantor set does not contain any open set.
Back
The definition of the Cantor set is as follows: let
and define, for each
n, the sets
A n
recursively as
-
A n = A n-1 \
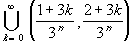
Then the Cantor set is given as:
-
C =
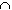 A n
A n
Another way to write the Cantor set is to note that each of the sets
A n can be written as a finite union of
2 n closed intervals, each of which has a length of
1 / 3 n, as follows:
- A 0 = [0, 1]
- A 1 = [0, 1/3]
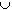 [2/3, 1]
[2/3, 1]
- A 2 = [0, 1/9]
 [2/9, 3/9]
[2/9, 3/9]
 [6/9, 7/9]
[6/9, 7/9]
 [8/9, 1]
[8/9, 1]
- ...
Now suppose that there is an open set
U contained in
C.
Then there must be an open interval
(a, b) contained in
C.
Now pick an integer
N such that
Then the interval
(a, b) can not be contained in the
set
AN, because that set is comprised of
intervals of length
1 / 3N. But if that interval
is not contained in
AN it can not be contained
in
C. Hence, no open set can be contained in the Cantor set
C.
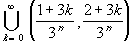
 A n
A n
 [2/3, 1]
[2/3, 1]
 [2/9, 3/9]
[2/9, 3/9]
 [6/9, 7/9]
[6/9, 7/9]
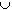 [8/9, 1]
[8/9, 1]
 Interactive Real Analysis
Interactive Real Analysis