5.2. Compact and Perfect Sets
Example 5.2.13(b): Properties of the Cantor Set
The definition of the Cantor set is as follows: let- A 0 = [0, 1]
-
A n = A n-1 \
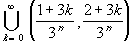
-
C =
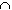 A n
A n
One way to do this is to note that each of the sets A n can be written as a finite union of 2 n closed intervals, each of which has a length of 1 / 3 n, as follows:
- A 0 = [0, 1]
- A 1 = [0, 1/3]
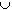 [2/3, 1]
[2/3, 1]
- A 2 = [0, 1/9]
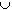 [2/9, 3/9]
[2/9, 3/9]
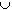 [6/9, 7/9]
[6/9, 7/9]
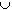 [8/9, 1]
[8/9, 1]
- ...
 C =
C =
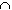 A n
Then x is in
A n for all n. If x is in
A n, then x must be contained in one of
the 2 n intervals that comprise the set
A n. Define
x n to be the left endpoint of that subinterval
(if x is equal to that endpoint, then let
x n be equal to the right endpoint of that
subinterval). Since each subinterval has length
1 / 3 n, we have:
A n
Then x is in
A n for all n. If x is in
A n, then x must be contained in one of
the 2 n intervals that comprise the set
A n. Define
x n to be the left endpoint of that subinterval
(if x is equal to that endpoint, then let
x n be equal to the right endpoint of that
subinterval). Since each subinterval has length
1 / 3 n, we have:
- | x - x n | < 1 / 3 n
Note that this proof is not yet complete. One still has to prove the assertion that each set A n is indeed comprised of 2 n closed subintervals, with all endpoints being part of the Cantor set. But that is left as an exercise.
Since every perfect set is uncountable, so is the Cantor.
 Interactive Real Analysis
Interactive Real Analysis