5.2. Compact and Perfect Sets
Example 5.2.13(a): Properties of the Cantor Set
The definition of the Cantor set is as follows: let- A 0 = [0, 1]
-
A n = A n-1 /
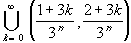
- C =
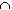 A n
A n
 is open. Since
A 0 is closed, the sets
A n are all closed as well, which can be shown by
induction. Also, each set
A n
is a subset of
A 0,
so that all sets
A n
are bounded.
is open. Since
A 0 is closed, the sets
A n are all closed as well, which can be shown by
induction. Also, each set
A n
is a subset of
A 0,
so that all sets
A n
are bounded.
Hence, C is the intersection of closed, bounded sets, and therefore C is also closed and bounded. But then C is compact.
 Interactive Real Analysis
Interactive Real Analysis