3.5. Special Sequences
Definition 3.5.7: Exponential Sequence
Proof:
We will use a simple substitution to prove this. Letx/n = 1/u, or equivalently, n = u xThen we have
But the term inside the square brackets is Euler's sequence, which converges to Euler's number e. Hence, the whole expression converges to ex, as required.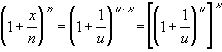
In fact, we have used a property relating to functions to make this proof work correctly. What is that property ?
If we did not want to use functions, we could first prove the statement for x being an integer. Then we could expand it to rational numbers, and then, approximating x by rational number, we could prove the final result.
 Interactive Real Analysis
Interactive Real Analysis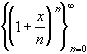 Exponential Sequence: Converges
to the exponential function ex = exp(x) for any
real number x.
Exponential Sequence: Converges
to the exponential function ex = exp(x) for any
real number x.