3.5. Special Sequences
Definition 3.5.2: Exponent Sequence
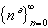 Exponent Sequence:
The convergence depends on the size of the exponent a:
Exponent Sequence:
The convergence depends on the size of the exponent a:
- a > 0: the sequence diverges to positive infinity
- a = 0: the sequence is constant
- a < 0: the sequence converges to 0
Exponent sequence with a = 2
Exponent sequence with a = -2
Proof:
Write n a = e a ln(n). Then:- if a > 0 then as n approaches infinity, the function ea ln(n) approaches infinity as well
- if a < 0 then as n approaches infinity, the function ea ln(n) approaches zero
- if a = 0 then the sequence is the constant sequence, and hence convergent
But actually we first need to understand exactly what na really means:
- If a is an integer, then clearly na means to multiply n with itself a times
- If a = p/q is a rational number, then np/q means to multiply n p times, then take the q-root
- It is unclear, however, what na means
if a is an irrational number. For example, what is
n
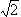 , or
n
, or
n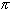 ?
?
na = ea ln(n)In that light, the original 'proof' was not bad after all, but of course we now need to know how exactly the exponential function is defined, and what its properties are before we can continue. As it turns out, the exponential function is not easy to define properly. Generally one can either define it as the inverse function of the ln function, or via a power series.
Another way to define na for a being rational it to take a sequence of rational numbers rn converging to a and to define na as the limit of the sequence {nrn}. There the problem is to show that this is well-defined, i.e. if there are two sequences of rational numbers, the resulting limit will be the same.
In either case, we will base our proof on the simple fact:
if p > 0 and x > y then xp > ypwhich seems clear enough and could be formally proved as soon as the exponential function is introduced to properly define xp.
Now take any positive number K and let n be an integer bigger than K1/a. Since
n > K1/awe can raise both sides to the a-th power to get
na > Kwhich means - since K was arbitrary - that the sequence {na} is unbounded.
The case a = 0 is clear (since n0 = 1). The second case of a < 0 is related to the first by taking reciprocals (details are left as an exercise). Since we have already proved the first case we are done.
 Interactive Real Analysis
Interactive Real Analysis