3.4. Lim Sup and Lim Inf
Examples 3.4.2(b):
What is
inf,
sup,
lim inf and
lim sup for
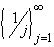
?
Back
Since this sequence is
{1, 1/2, 1/3, 1/4, ...} the infimum
is zero, while the supremum is 1. As for
lim inf and
lim sup, we find first the sequence of numbers
Aj and
Bj mentioned in the
definition.
- A1 = inf{1, 1/2, 1/3, 1/4, ...} = 0
- A2 = inf{1/2, 1/3, 1/4, 1/5, ...} = 0
- A3 = inf(1/3, 1/4, 1/5, 1/6, ...} = 0
and so on. Therefore, it is clear that
lim inf 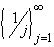 = 0
= 0
Similarly, we find the numbers
Bj= sup{aj, aj + 1, aj + 2, ...}:
- B1 = sup{1, 1/2, 1/3, 1/4, ...} = 1
- B2 = sup{1/2, 1/3, 1/4, 1/5, ...} = 1/2
- B3 = sup(1/3, 1/4, 1/5, 1/6, ...} = 1/3
and so on. Therefore, it is clear that
lim sup 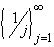 = 0
= 0
= 0
= 0
 Interactive Real Analysis
Interactive Real Analysis