2.4. The Real Number System
Theorem 2.4.5: Square Roots in R
Proof:
Since the above equation is not true in Q, we have to use a property of the real numbers that is not true for the rational numbers. Define the set- S = {
t
 R: t > 0 and
t2
R: t > 0 and
t2  2 }
2 }
S is not empty, because 1 is contained in S, and S is bounded above by, say, 5. Hence, using the least upper bound property of the real numbers, S has a least upper bound s:
- s = sup(S)
Now we hope that s2 = 2, i.e. s is the desired solution. Since 1 is in S, we know
- s > 1
- Is s2 < 2 ?
- Let
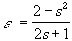 .
Then, by assumption 0 <
.
Then, by assumption 0 <  < 1,
so that
< 1,
so that
Hence, s +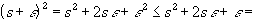
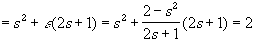
 is also in S,
in which case s can not be an upper bound for S. This is a
contradiction, so this case is not possible.
is also in S,
in which case s can not be an upper bound for S. This is a
contradiction, so this case is not possible.
- Is s2 > 2 ?
- Let
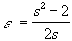 . Again
. Again
 > 0, so that
> 0, so that
Hence, s -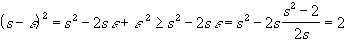
 is another upper
bound for S, so that s is not the least upper bound for
S. This is a contradiction, so that this case is not possible.
is another upper
bound for S, so that s is not the least upper bound for
S. This is a contradiction, so that this case is not possible.
 Interactive Real Analysis
Interactive Real Analysis