9. Historical Tidbits
9.10. Peano, Guiseppe (1858-1932)

Giuseppe Peano was born to a poor farming family in Spinetta, Italy, on August 27, 1858. Being born in such a poor village, he and his brother were forced to walk to the neighboring town of Cueno to attend school. However, this handicap did not stop him from excelling in his studies and he was sent to Turin with his uncle to finish his primary schooling. In 1876, he enrolled at the University of Turin to study engineering but later decided on mathematics. The university would be his home for the rest of his life. After graduating, he became a University Assistant in 1880, professor at the Royal Military Academy in 1886, extraordinary professor in 1890 and ordinary professor in 1895. In 1887, he was married but had no children.
For the first part of his life, mathematics dominated Peano's life. During this period, almost all of his mathematical discoveries were made. He proved that y' = f(x,y) on the sole condition that f is continuous and set the minimum conditions for second order partials of an equation to be equal. He was the first person to develop a space-filling curve, a one-dimensional curve that fills all the points in a two-dimensional space. He also developed independently a method of successive approximations for the solution of differential equations and developed the idea of the cluster point of a function. He was also an early supporter of the use of recursive functions and vectors.
Peano's greatest contributions, however, were in the fields of axiomatization of mathematics and mathematical logic . Axiomatization of mathematics is the development of the postulates (axioms) and definitions that are the basis of the mathematical system. His most famous set, known as Peano's postulates, put forth the axioms of natural numbers. In addition, he also developed a related set for geometry.
Mathematical logic is the use of symbols instead of words to write mathematical statements. The idea had
be raised over a century earlier by Leibniz who had suggested a universal language. By using symbols,
the equations are simplified and made easily understood to anyone, no matter what language they speak.
For example, Peano introduced the symbols 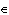 and
and 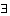 to represent "belongs to the set of" and "there exists" respectively. Mathematical logic quickly became
the focus of his work. In 1889, Peano published his first version of a system of mathematical logic in his
work Arithmetics principia, which included his famous axioms of natural numbers. Two years
later, he established a journal, the Rivista, in which he proposed the symbolizing of all
mathematical propositions into his system. The project, which became known as the Formulario,
became his focus for the next fifteen years. When it was finished in 1908, the book contained over 4200
symbolized formulas and theorems with proofs in only 516 pages. His work did not go unnoticed. He was
elected to the Academy of Sciences in Turin in 1891 and was a speaker at several International Congress
of Mathematics. In addition, he was honored by the Italian government with several knighthoods,
including the Order of the Crown of Italy.
to represent "belongs to the set of" and "there exists" respectively. Mathematical logic quickly became
the focus of his work. In 1889, Peano published his first version of a system of mathematical logic in his
work Arithmetics principia, which included his famous axioms of natural numbers. Two years
later, he established a journal, the Rivista, in which he proposed the symbolizing of all
mathematical propositions into his system. The project, which became known as the Formulario,
became his focus for the next fifteen years. When it was finished in 1908, the book contained over 4200
symbolized formulas and theorems with proofs in only 516 pages. His work did not go unnoticed. He was
elected to the Academy of Sciences in Turin in 1891 and was a speaker at several International Congress
of Mathematics. In addition, he was honored by the Italian government with several knighthoods,
including the Order of the Crown of Italy.
It was at this time that Peano became interested in the auxiliary language movement. This movement was one of the first efforts in attempting to develop a universal language understood by everyone, especially for the scientific community. Intrigued by the idea, he became active at the turn of the century and in 1908 he was elected director of the Academia pro Interlingua, a congress for the development of an auxiliary language. His proposal was called Latino sine flexione, a version of Latin stripped of all grammar. Because of his work in this field, his mathematical work ended almost completely.
It was at this time that Peano's career declined. Interlingua, as his universal language would eventually be named, failed to gain widespread acceptance because of the international popularity of English. The Formulario, though impressive in its accomplishment, found little interest in the mathematical community. This was partially because of the confusion over the symbols and partially because it was published in Latino sine flexione, which nobody really understood. Meanwhile, back at the university, opposition was mounting. Professors objected to his insistence that he teach all his students mathematical logic and the fact that he never gave examinations. Meanwhile, students resented having to learn "the symbols" when they never would use them in real life and labeled pupils that liked his classes as suffering from "Peanitis." In 1901, he was forced to resign from the military academy and was stripped of teaching all the engineering students at the university. Even after his death, there remained great opposition to the mathematician.
Despite all this, Peano was happy for the end of his life. He was active in organizations for primary and secondary education, developed a perpetual calendar and became politically involved in a cotton workers' strike, hosting a party for the strikers at his country villa. He died of a heart attack in Turin on April 20, 1932.
For related information on Peano, see: Peano axioms.
Sources
- Kennedy, Hubert C. Peano Life and Works of Giuseppe Peano. Boston: D. Reidel Publishing Company, 1980.
- Kennedy, Hubert C. "Peano, Giuseppe." Dictionary of Scientific Biography. New York: Charles Scribner's Sons, 1970. vol. 10, pp. 441-444.
 Interactive Real Analysis
Interactive Real Analysis