8.4. Taylor Series
Example 8.4.5: A Taylor Series that does not Converge to its Function
Define
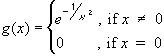 . Show that:
. Show that:
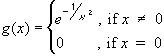 . Show that:
. Show that:
- The function is infinitely often differentiable
- The Taylor series Tg(x, 0) around c = 0 has radius of convergence infinity.
- The Taylor series Tg(x, 0) around c = 0 does not converge to the original function.
We have already shown before that:
- g is infinitely often differentiable
- g(n)(0) = 0 for all n
The Taylor series of g is therefore:
Tg(x, 0) =an xn =
1/n! g(n)(0) xn =
0 xn = 0 for all x
In particular, the radius of convergence is infinity. But the original function is not identically equal to zero (g(0) = 0 but g(x) > 0 for x # 0), so that:
Tg(x, 0) # g(x) unless x = 0
 Interactive Real Analysis
Interactive Real Analysis