6.6. A Function Primer
C(inf) Function
|
Zoom in with the mouse or click on Options to select different window dimensions. In particular, notice how smooth the function is at the origin: it is hardly distinguishable from the x-axis near zero. |
Can a polynomial have that property ? In other words, can you find a polynomial of any (fixed) degree such that it is not identically zero, yet all derivatives at x = 0 are zero ?
Proof:
This function is special, as we will see when dealing with power series representations: if one wants to find a power series representation, one could apply Taylor's formula to find the coefficients of the power series, say, centered at zero. That requires that the function under consideration has to be infinitely often differentiable. This function is. Taylor's formula involves derivatives of the function at the origin. In this case, they are all zero. Hence, the power series associated with this function would be identically equal to zero. But then it does not represent the original function.In other words, there are functions for which you can use Taylor's theorem to find a convergent power series, but this power series is not equal to the original function.
In any case, we will first prove that this function is once differentiable, with g'(0) = 0. Obviously, if x # 0, then g'(x) exists by the chain rule, and we have
Next, we need to find the derivative at x = 0 by looking at the limit of the difference quotient at x = 0for x not zero
This limit looks hard, but we can make the substitution u = 1 / x and use 'Hospital's rule: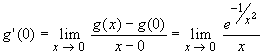
Note that we do have to look at u approaching positive and negative infinity, but because of the square term in the denominator we can deal with both cases in one line.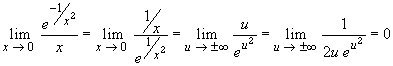
Therefore, g is differentiable at x = 0 and the derivative is zero. Next we need to show that g'(x) is continuous. It is obviously continuous for all x but zero, so we only need to check continuity at x = 0:
Again, we have used the above substitution, and we have applied l'Hospital's rule several times in our head. But the result is that g(x) is differentiable everywhere, and g'(0) = 0. Now we could treat the case N = 2, N = 3, and so forth. But we need to prove this for all N, so eventually we will have to employ an induction argument. Also, the computations of higher derivatives will become more and more complicated, since the product rule will introduce additional terms. Therefore, we have to look at the problem in a more abstract way.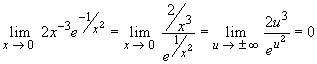
While the details are left as an exercise, you might want to make use of (and first prove) the following steps:
Let p(x) be a polynomial in 1 / x, i.e. 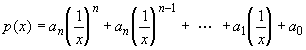 .
Then show the following:
.
Then show the following:
- the n-th derivative of g(x) for x not zero is of the form p(x)
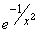
- the limit as x approaches zero of p(x)
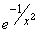 equals zero
equals zero
- the limit of the difference quotient at zero for functions of the form
p(x)
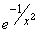 is zero
is zero
 Interactive Real Analysis
Interactive Real Analysis