4.2. Convergence Tests
Ratio Test
Consider the series 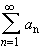 . Then
. Then
The ratio test is easier to use than the Root test . However, there are
series for which the ratio tests gives no information, but the root test
will. In that sense, the ratio test is weaker than the root test. In
addition, the ratio test can be proved using the root test, but not visa
versa.
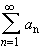 . Then
. Then
- if lim sup | a n+1 / a n | < 1 then the series converges absolutely.
- if there exists an N such that
| a n+1 / a n |
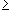 1 for all
n > N then the series diverges.
1 for all
n > N then the series diverges.
- if lim sup | a n+1 / a n | = 1, this test gives no information
Using the lim sup rather than the regular limit has the advantage that we don't have to worry about existence of the limit. However, if the regular limit exists, the lim sup yields the same number. Therefore, we loose nothing by looking at the limit superior.
| Example 4.2.16: | |
| |
Proof:
The proof is very similar to the proof of the root test:
Assume that
lim sup | a n+1 / a n | < 1:
because of the properties of the lim sup, we know that
there exists
 > 0 and
N > 1 such that
> 0 and
N > 1 such that
| a n+1 / a n | < 1 -for n > N. Multiplying both sides by a n we obtain
| a n+1 | < (1-for n > N. Therefore, we also have) | a n |
| a n+2 | < (1-for n > N. Repeating this procedure, we get, eventually, that) | a n+1 | < (1 -
) 2 | a n |
| a k | < (1 -for k > N. But the terms on the right hand side form a convergent geometric series, indexed using the variable k, where N is some constant integer. Hence, by the comparison test the series with terms on the left-hand side will converge absolutely.) k-N | a N |
The proof for the second case if left as an exercise.
 Interactive Real Analysis
Interactive Real Analysis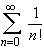 converge ?
converge ?
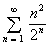 for convergence. Compare with the same example using the root test.
for convergence. Compare with the same example using the root test.
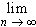 an/n! = 0
an/n! = 0