Divergence Test
Examples 4.2.2:
Does the Divergence test apply to show that the series
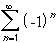 converges or diverges ? How about the series
converges or diverges ? How about the series
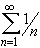 ?
?
The first series converges: to apply the divergence test, we
have to consider the sequence
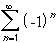 converges or diverges ? How about the series
converges or diverges ? How about the series
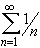 ?
?
which we have shown to diverge. In particular, the sequence does not converge to zero. Hence, the above series can not converge.j}.gif)
One can easily show directly that this series does not converge by looking at the sequence of partial sums.
For the second series, the divergence test does not apply. In order to use the divergence test, we need to check the limit of the sequence
{ 1/n }But this limit is indeed zero. Therefore, the divergence test does not give any information about this series.
In fact, this series is the harmonic series, and it can be shown to diverge.
 Interactive Real Analysis
Interactive Real Analysis