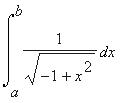7.2. Integration Techniques
Example 7.2.4(e): Applying the Substitution Rule
Now it gets interesting again. In a previous example we had the square root of r2 - x2, and we used the substitution x = sin(t) because of the equality sin2(t) + cos2(t) = 1.For the first integral we use the substitution
x = sinh(t) [ = 1/2 (et - e-t) ] so thatbecause of the hyperbolic trig equation
dx/dt = 1/2 (et + e-t) = cosh(t) or dx = cosh(t) dt
cosh2(t) - sinh2(t) = 1(which you should verify). With that substitution we have that:
where arc sinh is the inverse function of sinh. Note that it is not hard to show that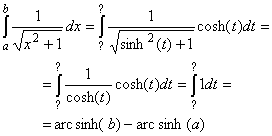
Evaluating the second integral is left as an exercise (try the substitution x = cosh(t)).
 Interactive Real Analysis
Interactive Real Analysis and
and