7.4. Lebesgue Integral
Example 7.4.11(d): Properties of the Lebesgue Integral
Suppose f is a bounded, non-negative function defined on a measurable
set E with finite measure such that
 E f(x) dx = 0.
Show that f must then be equal to zero except on a set of
measure zero.
E f(x) dx = 0.
Show that f must then be equal to zero except on a set of
measure zero.
Define the sets
 E f(x) dx = 0.
Show that f must then be equal to zero except on a set of
measure zero.
E f(x) dx = 0.
Show that f must then be equal to zero except on a set of
measure zero.
En = { xThenE: f(x)
1/n }
Z = { xE: f(x) # 0 }
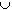 En = Z
and
En
En = Z
and
En 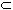 E.
Using the previous two examples we get:
E.
Using the previous two examples we get:
0 =so that m(En) = 0 for all n. But thenE f(x) dx
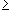
En f(x) dx
1/n m(En)
m(Z) = m(which is what we had to prove.En)

En = 0
 Interactive Real Analysis
Interactive Real Analysis