7.2. Integration Techniques
Example 7.2.6(b): Applying Integration by Parts
Find
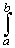 x2 cos(x) dx
x2 cos(x) dx
Back
This time we define
- g'(x) = cos(x) so that g(x) =
 cos(x) dx = sin(x)
cos(x) dx = sin(x)
- f(x) = x2 so that f'(x) = 2x
Then
G(x) = f(x) g(x) = sin(x) x2 and
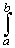 x2 cos(x) dx =
G(b) - G(a) -
x2 cos(x) dx =
G(b) - G(a) -
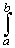 2x sin(x) dx
2x sin(x) dx
Intergration by parts reduced the original problem to finding a slightly simpler
integral, but we can not find the second integral immediately. What worked once
might work again so let's use integration by parts on the second integral with:
- g'(x) = sin(x) so that g(x) =
 sin(x) dx = -cos(x)
sin(x) dx = -cos(x)
- f(x) = 2x so that f'(x) = 2
so that
G*(x) = -2x cos(x). Therefore
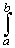 2x sin(x) dx =
G*(b) - G*(a) +
2
2x sin(x) dx =
G*(b) - G*(a) +
2 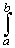 cos(x) dx
cos(x) dx
Taking everything together we have:
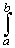 x2 cos(x) dx =
G(b) - G(a) - [G*(b) - G*(a) + 2
x2 cos(x) dx =
G(b) - G(a) - [G*(b) - G*(a) + 2 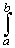 cos(x) dx ] =
cos(x) dx ] =
= G(b) - G(a) - G*(b) + G*(a) - 2 (sin(b) - sin(a)) =
= sin(b) b2 - sin(a) a2 + 2b cos(b) - 2a cos(a) -2sin(b) + 2sin(a)
cos(x) dx = sin(x)
x2 cos(x) dx = G(b) - G(a) -
2x sin(x) dx
sin(x) dx = -cos(x)
2x sin(x) dx = G*(b) - G*(a) + 2
cos(x) dx
x2 cos(x) dx = G(b) - G(a) - [G*(b) - G*(a) + 2
cos(x) dx ] =
 Interactive Real Analysis
Interactive Real Analysis