7.3. Measures
Example 7.3.3(b): Outer Measure of Intervals
Since outer measure should be related to 'length' we expect that the outer measure of [a, b] is b - a. Indeed, that is the case.
Take the interval
(a -  , b +
, b +  ).
That interval covers [a, b] so that
).
That interval covers [a, b] so that
m*([a, b])Sinceb - a + 2

 was arbitrary we have
was arbitrary we have
(*) m*([a, b])To show the other inequality, we must show that for any collection In of intervals whose union covers [a, b] we haveb - a
Take such a collection and assume, for the moment, that it is finite. Order that collection as follows:l(In)
b - a
- The first interval is the one that contains a. Call it (a1, b1).
- If b1 < b, then pick as the second interval that which contains b1. Call it (a2, b2).
- If b2 < b, then pick as the third interval that which contains b2. Call it (a3, b3).

Subintervals with k = 6
Then
Therefore, for any finite collection of open intervals In we have:l(In)
(b1 - a1) + (b2 - a2) + ... + (bk - ak) =
= -a1 + (b1 - a2) + (b2 - a3) + ... + (bk-1 - ak) + bk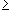
bk - a1
b - a
(**)Now take an arbitrary collection of intervals In that cover [a, b]. By the Heine-Borel theorem we can extract a finite subcover, i.e. a finite number of intervals that still cover [a, b]. We already know that for the finite subcover inequality (**) holds, and the sum for all intervals in the cover is even greater than the left side of (**). Therefore (**) holds for any collection of open sets covering [a, b], and thusl(In)
b - a
m*([a, b])b - a
That together with (*) show that m*([a, b]) = b - a, as required.
 Interactive Real Analysis
Interactive Real Analysis