7.3. Measures
Example 7.3.3(a): Outer Measure of Intervals
Since outer measure should be related to 'length' we expect that the outer measure of the empty set is zero. Indeed, that is the case.Take the open interval (-1/n, 1/n), whose length is 2/n. It covers the empty set, because the empty set is a subset of every set. Therefore m*(O) < 2/n for all n which implies that m*(O) = 0.
Now assume that A 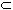 B.
Then every cover of B is also a cover of A, but not every
cover of A covers B. That means that there are more collections
to consider when computing m*(A) instead of
m*(B), so that the infimum in the first case is
smaller than in the second case.
B.
Then every cover of B is also a cover of A, but not every
cover of A covers B. That means that there are more collections
to consider when computing m*(A) instead of
m*(B), so that the infimum in the first case is
smaller than in the second case.
 Interactive Real Analysis
Interactive Real Analysis m*(B)
for all
A
m*(B)
for all
A