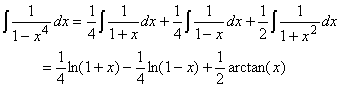7.2. Integration Techniques
Example 7.2.12(b): Integrating Rational Functions
Find the integral
 (1 - x4)-1 dx
(1 - x4)-1 dx
Back
We want to again use partial fraction decomposition, so we need to factor
the polynomial
p(x) = 1 - x4. Clearly:
1 - x4 = (1 - x2) (1 + x2) =
(1 + x) (1 - x) (1 + x2)
By the partial fraction decomposition theorem we therefore know that:
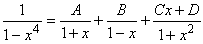
We can again combine the right side as follows:
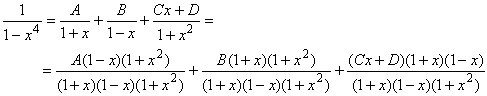
so that
1 = A (1-x)(1+x2) + B(1+x)(1+x2) + (Cx+D)(1-x2) =
= A + Ax2 - Ax - Ax3 +
B + Bx2 + Bx + Bx3) +
Cx - Cx3 + D - Dx2 =
= (A + B + D) + x(-A + B + C) + x2(A + B - D) + x3(-A + B - C)
for all
x. This gives four equations in four unknowns:
| A + B + D= 1 | (for the constant coefficient) |
| -A + B + C = 0 | (for the x coefficient) |
| A + B - D = 0 | (for the x2 coefficient) |
| -A + B - C = 0 | (for the x3 coefficient) |
which - perhaps after reviewing how to efficiently solve systems of linear equations -
gives the answer:
A = 1/4, B = 1/4, D = 1/2, C = 0
Therefore we can solve our original integral
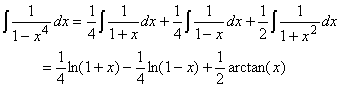
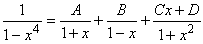
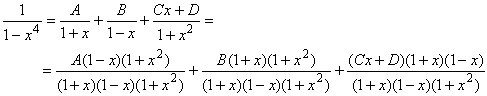
 Interactive Real Analysis
Interactive Real Analysis (1 - x4)-1 dx
(1 - x4)-1 dx