7.2. Integration Techniques
Example 7.2.12(a): Integrating Rational Functions
Find the integral
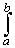 (1 - x2)-1 dx
(1 - x2)-1 dx
where the interval
[a, b] does not include 1 and -1.
Back
The polynomial
p(x) can be factored into
p(x) = 1 - x2 = (1 + x) (1 - x)
By the partial fraction decomposition theorem we know that:
1 / p(x) =
A / 1 + x + B / 1 - x
for some constants
A and
B. To find these
constants, we combine the two rational functions on the right side:
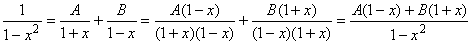
Therefore we must have:
1 = A (1 - x) + B (1 + x) = A + B + x(B - A)
for all
x. That gives two linear equations in two unknowns:
A + B = 1
B - A = 0
so that
A = B = 1/2. Now we can solve our original integral:
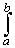 (1 - x2)-1 dx =
1/2
(1 - x2)-1 dx =
1/2 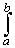 1/ (x + 1) dx -
1/2
1/ (x + 1) dx -
1/2 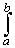 1/ (x - 1) dx =
1/ (x - 1) dx =
= 1/2 [ (ln(|b + 1|) - ln(|a + 1|)) - (ln(|b - 1|) - ln(|a - 1|))]
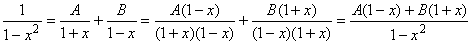
(1 - x2)-1 dx = 1/2
1/ (x + 1) dx - 1/2
1/ (x - 1) dx =
 Interactive Real Analysis
Interactive Real Analysis