8.4. Taylor Series
Theorem 8.4.6: Taylor's Theorem
Suppose f 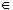 Cn+1([a, b]),
i.e. f is (n+1)-times continuously differentiable
on [a, b]. Then, for
c
Cn+1([a, b]),
i.e. f is (n+1)-times continuously differentiable
on [a, b]. Then, for
c 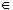 [a,b] we have:
[a,b] we have:
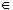 Cn+1([a, b]),
i.e. f is (n+1)-times continuously differentiable
on [a, b]. Then, for
c
Cn+1([a, b]),
i.e. f is (n+1)-times continuously differentiable
on [a, b]. Then, for
c 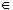 [a,b] we have:
[a,b] we have:
f(x) =where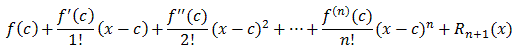
Rn+1(x) = 1/n!In particular, the Taylor series for an infinitely often differentiable function f converges to f if and only if the remainder R(n+1)(x) converges to zero as n goes to infinity.(x-t)nf (n+1)(t) dt
The statement involves "all integers" and therefore an induction proof might be in order. By the fundamental theorem of calculus we know that
f '(t) dt = f(x) - f(c)
f(x) = f(c) +f '(t) dt
That proves the base case n=0 of our induction. Now assume that
f(x) =where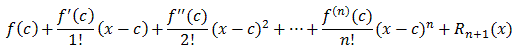
Rn+1(x) = 1/n!(x-t)nf (n+1)(t) dt
is true. Let's look at the term Rn+1(x) and integrate by parts, where:
u'(t) = (x-t)n 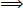
u(t) = - 1/n+1 (x-t)n+1 v(t) = f (n+1)(t) 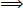
v'(t) = f (n+2)(t)
Therefore
Rn+1(x) = 1/n!(x-t)nf (n+1)(t) dt =
= 1/n!u'(t) v(t) dt =
= 1/n! (u(x)v(x) - u(c)v(c) -u(t) v'(t) dt) =
= 1/n! 1/n+1 (x-c)n+1 f (n+1)(c) + 1/n! 1/n+1(x-t)n+1 f (n+2)(t) dt =
= 1/(n+1)! (x-c)n+1 f (n+1)(c) + Rn+2(x)
But then, putting that together with our assumption, we have:
f(x) ==
=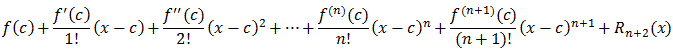
which finishes the induction.
It remains to show that the Taylor series for an infinitely often differentiable function f converges to f if and only if the remainder R(n+1)(x) converges to zero as n goes to infinity.
But what little there is to do to prove that is left to ... yup ... the reader.
 Interactive Real Analysis
Interactive Real Analysis