Interactive Real Analysis

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 7. The Integral
• 8. Sequences of Functions
• 8.1. Pointwise Convergence
• 8.2. Uniform Convergence
• 8.3. Series and Power Series
• 8.4. Taylor Series
• 8.5. Approximation Theory
• 9. Historical Tidbits
• Java Tools

8.4. Taylor Series

Proposition 8.4.8: Lagrange's Version of Taylor Remainder

Suppose f Cⁿ⁺¹([a, b]), i.e. f is (n+1)-times continuously differentiable on [a, b]. Then, for c [a,b] we have:

f(x) =

where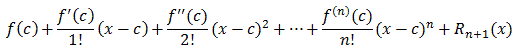

R_(n+1)(x) =

for some t between x and c.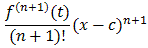

Context

Taylor's theorem gives us this result, except for the remainder, which is different. What we have to show, therefore, is that Taylor's remainder and the Lagrange remainder are really the same. In other words we need to show that:

R_n+1(x) = ¹/_n! (x-t)ⁿf ⁽ⁿ⁺¹⁾(t) dt =

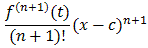
But this follows directly from the mean value theorem for integration (make sure to provide the details).