8.4. Taylor Series
Proposition 8.4.10: The Geometric Series
For the geometric series we can actually compute the remainder in Taylor's theorem exactly. Recall that we have previously shown that if we define Sn(x) = 1 + x + x2 + ... + xn we can find a closed form for Sn(x) by multiplying Sn(x) by x and then subtracting Sn(x) - x Sn(x) to get:
Sn(x) = 1-xn+1/1-x
or equivalently
1 + x + x2 + ... + xn = 1 - xn+1/1 - x = 1/1-x - xn+1/1-x
We can rearrange the terms to get:
1/1-x - (1 + x + x2 + ... + xn) = xn+1/1-x
But this means that we have (with c = 0)
|f(x) -| = |Rn+1(x)| = | xn+1 / 1 - x |
Thus, we have found the remainder exactly! And since |x| < 1 it is now clear that this remainder converges to zero, so that by Taylor's theorem the Taylor series converges to the function, as required.
 Interactive Real Analysis
Interactive Real Analysis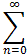 xn
for -1 < x < 1
xn
for -1 < x < 1