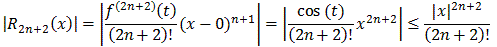8.4. Taylor Series
Proposition 8.4.12: Taylor Series for the Cosine Function
Taking derivatives at c=0 we quickly see that all odd derivatives at c=0 are zero while the even ones are plus or minus one. Thus:
cos(x) = 1 - 1/2! x2 + 1/4! x4 - ... + (-1)n/(2n)! x2n + R2n+2(x)
We need to show that the remainder R2n+2 goes to zero as n goes to infinity. Let's use the Lagrange remainder with c=0:
But for a fixed x we have already shown before that for any fixed number x
|x|n/n! = 0
which finishes the proof.
Fun Facts:
- cos(0) = 1
- cos is an even function, i.e. cos(-x) = cos(x)
- cos(x -
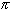 /2) = -sin(x)
/2) = -sin(x)  cos(x) = - sin(x)
cos(x) = - sin(x)
The fun facts are all easy and are left as exercises. For the third fact you
might start with f(x)=sin(x) and develop that in a series around
c = 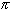 /2.
/2.
 Interactive Real Analysis
Interactive Real Analysis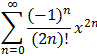 for all x
for all x