8.4. Taylor Series
Proposition 8.4.16: Taylor Series for the Arc Tan
arctan(x) = x - 1/3 x3 + 1/5 x5 - 1/7 x7 + ... =Note that the series converges at both endpoints.for |x|
1
Just as with the series representation of ln(1+x) we would start with a geometric series and integrate both sides. The details are left to you .... the boundary points |x| = 1 are an application of Abel's Limit theorem, which you should be able to do as well.
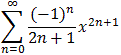
f(x) = arctan(x)
Fun Facts:
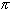 /4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
Since tan(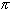 /4) = 1 we have
arctan(1)=
/4) = 1 we have
arctan(1)=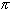 /4. Thus, this
statement follows from the above representation for x = 1.
/4. Thus, this
statement follows from the above representation for x = 1.
Series approaching Pi/4=0.785398
 Interactive Real Analysis
Interactive Real Analysis