8.3. Series and Power Series
Theorem 8.3.10: Differentiating and Integrating Power Series
Let
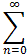 an (x - c)n
be a power series centered at c with radius of convergence
r > 0. Then:
an (x - c)n
be a power series centered at c with radius of convergence
r > 0. Then:
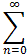 an (x - c)n
be a power series centered at c with radius of convergence
r > 0. Then:
an (x - c)n
be a power series centered at c with radius of convergence
r > 0. Then:
- The power series represents a continuous function for |x-c| < r
- The power series is integrable and can be integrated term-by-term for all |x - c| < r, i.e.

an (x - c)n dx =
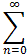
an (x - c)n dx =
1/n+1 an (x - c)n+1 + const
- The power series is differentiable and can be differentiated term-by-term for all |x - c| < r, i.e.
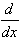
an (x - c)n =
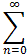
an (x - c)n =
n an (x - c)n-1
 Interactive Real Analysis
Interactive Real Analysis