8.2. Uniform Convergence
Definition 8.2.1: Uniform Convergence
 > 0 there is a positive
integer N such that
> 0 there is a positive
integer N such that
| fn(x) - f(x) | <for all x
D whenever n
N
Please note that the above inequality must hold for all x
in the domain, and that the integer N depends only on
 .
.
We should compare uniform with pointwise convergence:
- For pointwise convergence we could first fix a value for x and then choose N. Consequently, N depends on both
and x.
- For uniform convergence fn(x) must be uniformly close to f(x) for all x in the domain. Thus N only depends on
but not on x.
Let's illustrate the difference between pointwise and uniform convergence graphically:
Pointwise Convergence Uniform Convergence For pointwise convergence we first fix a value x0. Then we choose an arbitrary neighborhood around f(x0), which corresponds to a vertical interval centered at f(x0).
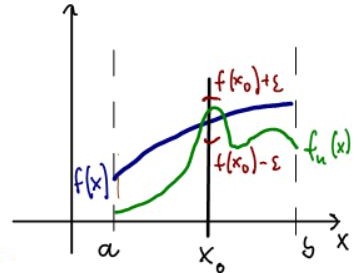
Finally we pick N so that fn(x0) intersects the vertical line x = x0 inside the interval (f(x0) -
, f(x0) +
)
For uniform convergence we draw an
-neighborhood around the entire limit function f, which results in an "
-strip" with f(x) in the middle.
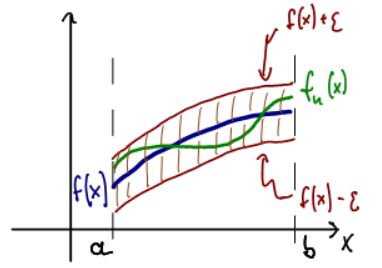
Now we pick N so that fn(x) is completely inside that strip for all x in the domain.
 Interactive Real Analysis
Interactive Real Analysis