8.3. Series and Power Series
Example 8.3.4 (b): Function Series Examples
|
Let's compute the sup-norm: || 32nxn ||[-r, r] = (9r)n The numeric series
Thus, our series converges absolutely and uniformly to a continuous function on every closed subset of (-1/9, 1/9). |
 Interactive Real Analysis
Interactive Real Analysis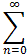 32nxn
represent a continuous function?
32nxn
represent a continuous function?