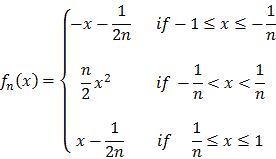8.2. Uniform Convergence
Example 8.2.6 (b): Uniform Convergence does not imply Differentiability
Find a sequence of differentiable functions that converges uniformly to a
continuous limit function but the limit function is not differentiable
Before we found a sequence of differentiable functions that
converged pointwise to the continuous, non-differentiable function f(x) = |x|.
Recall:
|
|
|
That same sequence also converges uniformly, which we will see by looking at ` || fn - f||D. We will find the sup in three steps:
- If 1
x
-1/n:
- | fn(x) - f(x)| = |-x - 1/2n + x| = 1/2n
- If -1/n < x < 1/n:
- |fn(x) - f(x)|
|n/2 x2| + |x|
n/2 1/n2 + 1/n = 3/2n
- If 1/n
x
1:
- | fn(x) - f(x)| = |x - 1/2n - x| = 1/2n
Thus, || fn - f||D < 3/2n which implies that fn converges uniformly to f. Note that all fn are continuous so that the limit function must also be continuous (which it is). But clearly f(x) = |x| is not differentiable at x=0.
 Interactive Real Analysis
Interactive Real Analysis