8.2. Uniform Convergence
Example 8.2.2 (b): Pointwise vs Uniform Convergence
Let fn(x) = xn with domain
D = [0, 1]. Show that
{ fn(x) } converges pointwise but not uniformly.
What if we change the domain slightly to D = (0, 1)?
|
Let Then:
Hence fn(x) |
|
Uniform convergence on [0, 1] will fail, just by looking at the picture, because the difference between f(1)=1 and fn(x) = xn for x < 1 will get larger and larger. In fact, it won't matter if we take the closed interval [0, 1] or the open one (0, 1) because:
Take, say,  =1/2 and let
x < 1. Assume there exists an integer N such
that
=1/2 and let
x < 1. Assume there exists an integer N such
that
|fn(x) - f(x)| = | xn | < 1/2 for all n > NThen in particular | xN+1 | < 1/2 for some fixed N. But if we now pick x such that
1 > x > (1/2)1/N+1we have a contradiction.
 Interactive Real Analysis
Interactive Real Analysis
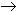 f(x)
pointwise for each fixed x.
f(x)
pointwise for each fixed x.