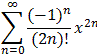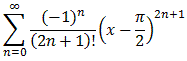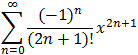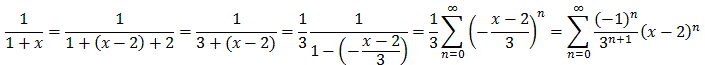8.4. Taylor Series
Example 8.4.4 (b): Taylor Series
If the given function had a convergent Taylor series, what would it be:
- f(x) = ex around c = 0 and f(x) = ex around c = 1
- g(x) = cos(x) around c = 0 and g(x) = cos(x) around c = Pi/2
- h(x) = sin(x) around c = 0
- k(x) = 1/1+x around c = 2
In each case we need to find
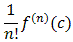 for the
given function at the specified center. We therefore compute derivatives
until we detect a pattern. Once we see the pattern we have the general
coefficient an and we can write down our
Taylor series.
for the
given function at the specified center. We therefore compute derivatives
until we detect a pattern. Once we see the pattern we have the general
coefficient an and we can write down our
Taylor series.
1. f(x) = ex
The pattern is clear ... it remains to divide by n! to get the an:
c=0 c=1 f(x) = ex f(0) = 1 f(1) = e f '(x) = ex f '(0) = 1 f '(1) = e ... f (n)(x) = ex f (n)(0) = 1 f (n)(1) = e
- Tf(x, 0) =
1/n! xn
- Tf(x, 1) =
e/n! (x-1)n
2. g(x) = cos(x)
The pattern now repeats so that:
c=0 c=Pi/2 f(x) = cos(x) f(0) = 1 f(Pi/2) = 0 f '(x) = -sin(x) f '(0) = 0 f '(Pi/2) = -1 f ''(x) = -cos(x) f ''(0) = -1 f ''(Pi/2) = 0 f '''(x) = sin(x) f '''(0) = 0 f '''(Pi/2) = 1 ...
- Tf(x, 0) = 1 + 0 x - 1/2! x2 + 0 x3 + 1/4! x4 + ... =
- Tf(x, 1) = 0 - 1/1! x + 0 x2 + 1/3! x3 + 0 x4 + ... = -
3. h(x) = sin(x)
The pattern now repeats so that:
c=0 f(x) = sin(x) f(0) = 0 f '(x) = cos(x) f '(0) = 1 f ''(x) = -sin(x) f ''(0) = 0 f '''(x) = -cos(x) f '''(0) = -1 ...
- Tf(x, 0) = 0 + 1 x + 0 x2 + 1/3! x3 + 0 x4 + ... =
Note that if we substitute x - Pi/2 for x and add a minus sign, we get the second series in the second example. That actually proves a trig identity - which one ?
4. k(x) = 1/1+x
c=2 f(x) = 1/1+x f(0) = 1/3 f '(x) = -1/(1+x)2 f '(0) = -1/32 f ''(x) = 1*2/(1+x)3 f ''(0) = 2!/33 f '''(x) = -1*2*3/(1+x)4 f '''(0) = -3!/34 ... f (n)(x) = (-1)n n!/(1+x)n+1 f (n)(0) = (-1)n n!/3n+1
Thus
Note that we can arrive at the same answer using our - by now familiar - geometric series and some appropriate substitution:
- Tf(x, 2) =
(-1)n / 3n+1 (x-2)n
 Interactive Real Analysis
Interactive Real Analysis