8.3. Series and Power Series
Example 8.3.9 (c): Power Series Center
This series has center of convergence c = -2 and, as you can confirm, radius r = 2. Thus, it converges for
|x + 2| < 2
In particular, the series diverges for x = 0, one of the endpoints of this interval.
But if we could find a series centered at c = 0 it would, in particular, converge at its center. But since we already know the original series does not converge for x = 0 we can not rewrite it with c=0 as center.
 Interactive Real Analysis
Interactive Real Analysis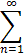 2-n (x+2)n
Why can you not re-center this series at c = 0?
2-n (x+2)n
Why can you not re-center this series at c = 0?