8.4. Taylor Series
Example 8.4.18 (e): Finding Taylor Series by Multiplication
Multiply two known series together until a pattern emerges.
Let's start with f(x) = x2 e2x. We know
the series for the exponential function ex, so by
substitution we also know e2x. Then we multiply
through by x2 to get the answer:
Example
- Find the Taylor series centered at zero for f(x) = x2 e2x.
- Find the first 3 terms of the Taylor series centered at zero for g(x) = sin(2x) ex2
x2 e(2x) = x21/n! (2x)n =
= x2 (1 + (2x) + 1/2! (2x)2 + 1/3! (2x)3 + 1/4! (2x)4 + ... ) =
= x2 (1 + 2 x + 1/2! 22 x2 + 1/3! 23 x3 + 1/4! 24 x4 + ... ) =
= x21/n! 2n xn =
=2n/n! xn+2
Now let's move on to g(x) = sin(2x) ex2. We could, of course, take derivatives at x = 0, but because of product and chain rule they quickly get out of hand. Therefore, we will try another method: multiplication with an "infinite" distributive law. We know:
sin(x) =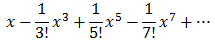
ex =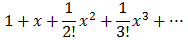
Substituting and multiplying we therefore get:
sin(2x) ex2 ==
==
==
==
=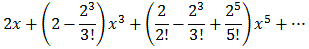
This approximation is not bad as you can see when you overlay the two functions. The red curve below shows the original function, the blue one shows the first three terms from the Taylor serires.
Of course the polynomial is much simpler than the original function, yet both functions are pretty close to each other if x is small.
 Interactive Real Analysis
Interactive Real Analysis