8.4. Taylor Series
Example 8.4.18 (c): Finding Taylor Series by Differentiation
Start with a known series and differentiate both sides.
Example
Find a series for f(x) = 2x/(1-x2)2This time we need to find a function whose derivative is our function in question, and whose Taylor series we know. Experimenting on scratch paper for a little while will give us, as a guess, the function
g(x) = 1/1-x2
The derivative of this function is g'(x) = 2x/(1-x2)2, our function in question. Thus:
f(x) = g'(x) =g(x) =
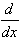
x2n =
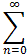
x2n =
2n x2n-1
for |x| < 1. We have, of course, quietly used substitution for the Geometric series and as a result - voila! - we have a Taylor series centered at zero for our function, just as desired.
2n x2n-1
f(x) = 2x/(1-x2)2
 Interactive Real Analysis
Interactive Real Analysis