8.3. Series and Power Series
Example 8.3.2 (a): Function Series Examples
Show that for a fixed
x 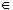 (-1, 1) the series
(-1, 1) the series
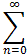 xn
converges pointwise to the function
f(x) = 1/1-x.
xn
converges pointwise to the function
f(x) = 1/1-x.
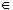 (-1, 1) the series
(-1, 1) the series
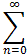 xn
converges pointwise to the function
f(x) = 1/1-x.
xn
converges pointwise to the function
f(x) = 1/1-x.
Once we fix a value of x the series (and the proof) is exactly the same as our regular old Geometric Series. There we used an a, now we use an x. But since repetition is helpful for memorization in long-term "storage", let's repeat the standard proof for convergence of the geometric series. Let
SN = 1 + x + x2 + ... + xN
be the N-th partial sum. Then
x SN = x(1 + x + x2 + ... + xN) = x + x2 + ... + xN + xN+1
But then
SN - x SN = SN(1 - x) = 1 - xN+1
Thus we have
SN = 1 - xN+1/1-x
Now we can take limits as N goes to infinity:
- if |x| < 1 the term xN+1 goes to zero
- if |x| > 1 the term xN+1 diverges
which finishes the proof.
 Interactive Real Analysis
Interactive Real Analysis