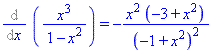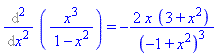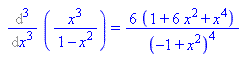8.4. Taylor Series
Example 8.4.2 (c): Derivatives of Power Series
Find the 10th and 11th derivative at zero for the function
f(x) = x3/1-x2. As a
hint, try to get the geometric series function involved somehow.
The obvious first try is to take 10 derivatives, then substitute x=0. Let's take a few derivatives:
This is getting out of hand - the derivatives are getting more and more complicated. Being notoriously lazy, the good mathematician looks for a short-cut. The hint mentions the geometric series ... recall
1/1-x = 1 + x + x2 + x3 + ...
Substituting x2 and multiplying by x3 gives us:
x3/1-x2 = x3(1 + x2 + x4 + x6 + ... ) =
= x3 + x5 + x7 + x9 ...
Comparing this with the coefficients of a power series we get:
a0 = a1 = a2 = 0
a3 = a5 = a7 = ... = 1
a4 = a6 = a8 = ... = 0
Since an = 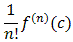 , or
equivalently f (n)(c) = n! an, we have our
answer:
, or
equivalently f (n)(c) = n! an, we have our
answer:
- f (10)(0) = 10! a10 = 0
- f (11)(0) = 11! a11 = 11! = 39,916,800
 Interactive Real Analysis
Interactive Real Analysis