8.4. Taylor Series
Example 8.4.2 (b): Derivatives of Power Series
Assume again that f(x) = e2x has a convergent power series
expression, but this time centered at c = 1. Find the coefficients
of this power series.
This time we assume our function can be represented as
e2x =an(x-1)n = = a0 + a1(x-1) + a2(x-1)2 + a3(x-1)3 + ...
Then, as before
an =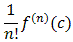
Again we need to find the n-th derivative of the function f at the center of the series. Taking derivatives on both sides and substituting 1 (the center in this example) we get:
n=0 f(x)=e2x f(1)=e n=1 f '(x)=2 e2x f '(1)=2 e2 n=2 f ''(x)=22e2x f ''(1)=22 e2 n=3 f (3)(x)=23e2x f (3)(1)=23 e2
Therefore, if e2x had a series representation centered at c = 1 it would be:
e2x =2n/n! e2 (x-1)n
 Interactive Real Analysis
Interactive Real Analysis