8.2. Uniform Convergence
Example 8.2.9: Convergence Almost Everywhere
Let rn be the (countable) set of rational numbers inside the interval [0, 1], ordered in some way, and define the functions
Show the following:and
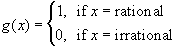
- The sequence gn converges pointwise to g but the sequence of Riemann integrals of gn does not converge to the Riemann integral of g.
- The sequence gn converges a.e. to zero and so does the sequence of Lebesgue integrals of gn.
Each gn is continuous except for finitely many points of discontinuity. But then each gn is integrable and it is easy to see that
gn(x) dx = 0
But the limit function is not Riemann-integrable and hence the sequence of Riemann integrals does not converge to the Riemann integral of the limit function.
Please note that while each gn is continuous except for finitely many points, the limit function g is discontinuous everywhere
On the other hand, each gn is zero except on a set of measure zero, and so is the limit function . Thus, using Lebesgue integration we have that all integrals evaluate to zero. But then, in particular, the sequence of Lebesgue integrals of gn converge to the Lebesgue integral of g.
 Interactive Real Analysis
Interactive Real Analysis